Problemas de Otimização
Um edifício com base retangular de deve ser construído num lote com lados paralelos ao do edifício, sendo exigido recuos de na frente e no fundo, e recuos de nas laterais. Ache as dimensões do lote com menor área onde esse edifício pode ser construído.
Passo 1
Vamos entender o que está acontecendo: a área do edifício vale , mas não sei quanto valerá cada um dos seus lados. O terreno onde será construído o prédio temos que deixar uma margem de para a frente e para o fundo. Dos lados, uma margem de . Assim, o esquema da situação pode ser esboçado assim:
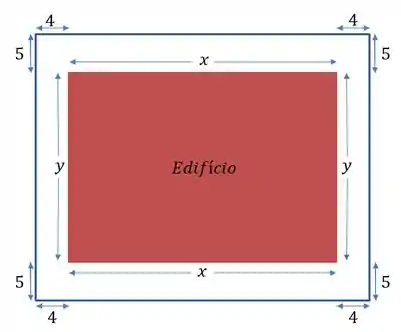
Como dito, a área do edifício será o produto de suas dimensões, que eu chamei de e , e valerá :
A função que queremos otimizar é a área total, com dimensões dadas por e por :
Isolando uma variável na primeira equação ficamos assim:
Passo 2
Agora que achamos uma equação podemos otimizá-la, derivando e igualando a :
Como as dimensões devem ser positivas,
Com isso, observando ainda que para valores menores que temos negativo e para valores maiores ele é positivo, vemos que consiste num ponto de mínimo!
As dimensões desse campo de área mínima serão:
Será um campo de dimensões x!