Encontre o ponto sobre a curva que está mais próximo do ponto
Passo 1
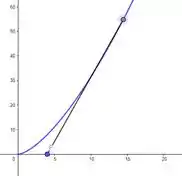
Bora lá então! A melhor forma da gente começar essa questão de enunciado beeem minimalista é tentar visualizar graficamente. A questão da curva e da ponto, então vamos fazer um esboço só pra pescar a ideia. No meu caso aqui como eu tenho uma ferramenta gráfica, vai ficar lindíssima a figura hahaha, dá uma olhada:
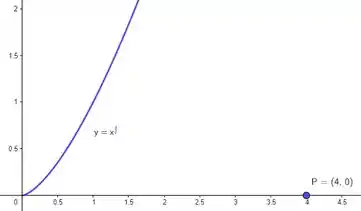
A distância ponto-curva nada mais é do que um segmento de reta que sai de e toca na curva. Só que, concorda comigo, que tem infinitas formas de eu desenhar esse segmento? Não? Então olha só três dessas infinitas formas:
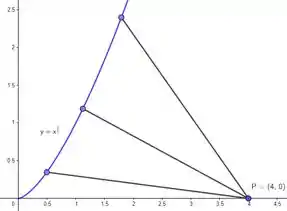
O que a questão pede é o menor segmento de reta dentre esses infinitos aí! Pra gente fazer isso, vamos precisar minimizar uma função distância reta-curva, que vamos chamar de . Vamos modelar então!
Passo 2
Show, pra modelar então, vamos pegar uma dessas retas quaisqueres possíveis. Note que eu posso chamar qualquer ponto sobre a curva de já que não especifiquei as coordenadas dele:
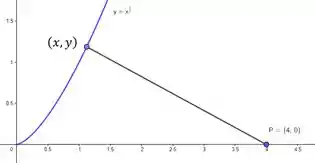
E olha só! Se eu projetar as coordenadas desse ponto, eu desenho um triângulo!
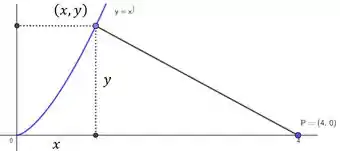
E é aqui que entra a magia da modelagem de ! Olha só que lindo, é a hipotenusa desse triângulo! Ele montadinho como acima, fica tranquilo de ver que ele tem altura e base . Sendo assim, por Pitágoras:
Como e porque se trata de uma dimensão física, temos:
Passo 3
E agora a gente parte pro cálculo mesmo. Achamos já o tamanho do segmento de reta em função da escolha do ponto de apoio sobre a curva. Pra achar o valor de que minimiza o tamanho da reta a gente deriva e iguala a zero! Usando Regra da Cadeia, temos:
Como essa função só zera quando o numerador zera, temos:
O que, por Bháskara, podemos reescrever para:
E logo:
Sendo as raízes de , ou seja, os pontos que satisfazem , temos esses dois pontos como os pontos que zeram o numerador de e logo, o próprio . Maaaaaaas, como um desses pontos é negativo e estamos falando de grandezas físicas, o único ponto que interessa a gente é o positivo, e logo:
E cabamos! A questão pediu pra encontre o ponto sobre a curva que está mais próximo do ponto . Achamos a coordenada desse ponto logo acima, pra achar a basta fazer:
As coordenadas serão:
Passo 4
Nesse último passo, vou só ser preciosista com um detalhe! O ponto que achamos pode ou pode não ser um ponto de mínimo, então é sempre bom checar! Pela natureza do nosso problema, se eu fizesse o seguinte limite, ia achar uma distância infinita.
Ou se fizesse o limite pra zero, ia achar uma distância , que é maior que :
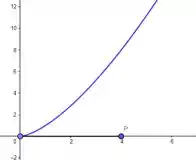
Da pra comprovar o resultado desses limites tanto grafica quanto visualmente. De fato, é o menor segmento de reta que conseguimos!