3) Determine o maior volume possível que pode conter uma caixa (paralelepípedo) com base quadrada, construída com de material, e que não inclui a tampa.
Passo 1
Um bom primeiro passo é desenhar a figura a ser otimizada e dar nome aos bois. Saca só:
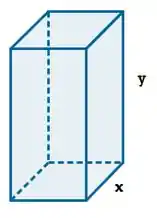
Sendo assim, como a base é quadrada, o volume dessa caixa é:
Ok, mas isso aí tem duas variáveis! Não da pra otimizar! Verdade, então vamos relacionar essas variáveis. Veja bem, a área das faces é:
Como temos nesse paralelepípedo quadrado (lembrando que não está inclusa a tampa da caixa) e retângulos, a área total é dada por:
Só que a área total é um dado do problema em! Então substituindo:
E juntando esse isolado na fórmula do volume, temos:
Passo 2
Show de bola, temos a função volume pronta pra ser otimizada. Como pra acharmos os pontos críticos precisamos derivar e igualar a , é exatamente isso que vamos fazer agora. Então bora:
Opa, um ponto crítico só! O volume para esse ponto crítico vai ser:
Passo 3
Só pra garantir que esse volume é mesmo o volume que maximiza, vamos testar as fronteiras. O valor de não é fixo, pode variar de até (só não pode ser negativo né, já viu quadrado com lado negativo?). Testando esses valores então:
Então realmente é o ponto que maximiza o volume!