Dentre todos os triângulos isósceles de perímetro conhecido, determine aquele que possui a maior área.
Passo 1
Bom, vou começar esboçando um triângulo isósceles (dois lados iguais) bem como suas principais dimensões (os lados e a altura).
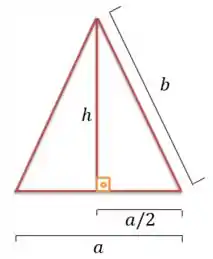
Ok, nós sabemos que para todos os triângulos a área é dada assim:
Queremos, nessa situação, a área máxima e qual configuração nos daria isso; se configurou um problema de otimização. Precisamos juntar a equação em função de uma só variável.
Só que não temos absolutamente nenhuma informação direta sobre essas variáveis. Porém temos duas relações, uma dada e uma do desenho, que podem nos ajudar a juntar tudo que queremos. Primeiro, sobre o perímetro conhecido (vou chamar de uma constante P):
Segundo, sobre o triângulo retângulo da figura:
Agora, vamos isolar em , jogar esse valor em e nela isolamos .
Sendo uma constante, temos então em função de . Para finalizar essa análise jogamos tudo na equação da área:
Ok, agora como fazemos para descobrir essa configuração máxima? Derivamos e igualamos essa equação da derivada da área a . Vamos usar aí a Regra do Produto e da Cadeia:
Beleza, descobrimos o valor de . E o de ? Vamos jogar na equação do perímetro:
Pera aí, deu igual ao ? Como assim, tem alguma coisa errada...
Aí que está, o resultado está certíssimo! A conclusão da questão é justamente essa:
O triângulo isósceles de maios área, dado certo perímetro, é um equilátero de lado !
Deu um trabalhinho, mas a questão é bem maneira, po!