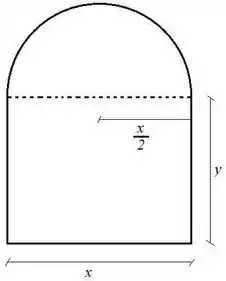
Uma janela é construída com um semicírculo e um retângulo como na figura abaixo. Sabendo que seu perímetro é , determine as dimensões da janela para que sua área seja máxima.
Passo 1
A figura e as dimensões já estão no enunciado, a próxima coisa a fazer aqui é achar as relações que o enunciado nos deu, primeiro pelo perímetro
Isso apareceu porque é a soma dos lados do retângulo mais aquele semicírculo,
A área vai ser
Que é a área do retângulo mais a área do semicírculo
Passo 2
Vamos agora escrever a função a ser maximizada em função de uma das variáveis do problema, vamos deixar a área em função de que as contas vão ser mais fáceis
Pela equação do perímetro vamos ter
Substituindo na equação da área
Passo 3
Agora temos que derivar essa função e igualar a
Vamos agora para o valor de
Substituindo o valor de vamos ter
Passo 4
Temos agora que ver se o ponto que achamos é de máximo local ou global. No fundo se existe algum ponto melhor. Para isso, teste os extremos do intervalo ou estude o comportamento da função.
Vamos analisar a função:
Repare que a função é um polinômio de segundo grau, e portanto, é uma parábola voltada para baixo e só possui um ponto de máximo que foi o que encontramos anteriormente, logo aquele ponto é o ponto onde a área é máxima
E eles vão ser as dimensões das janelas