Seja uma reta passando pelo ponto com inclinação negativa. Dentre todos os triângulos retângulos obtidos tomando e a interseção da reta com o primeiro quadrante, encontre as dimensões do que possui a menor hipotenusa.
Passo 1
Esta questão merece um desenho bem feito:
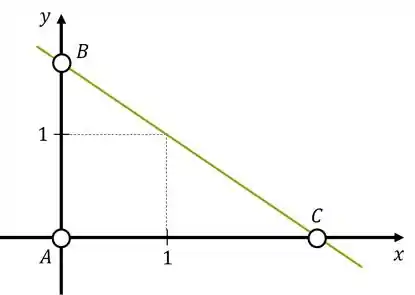
Agora sim podemos começar à pensar. Atribuindo algumas dimensões ao problema, sejam e os pontos:
Passo 2
Temos que a reta liga à e podemos encontrar sua equação, o que vai nos dar uma relação entre e . A reta tem equação:
Sabendo que passa por :
Passo 3
Também sabemos que ela passa pelo ponto :
Passo 4
Substituindo tudo:
Além disso, ela passa pelo ponto , logo:
Obs.: Note que .
Passo 5
Agora sim temos nossa relação. Desejamos minimizar a hipotenusa, que por Pitágoras tem comprimento:
Substituindo a relação entre eles:
Passo 6
O mínimo é um ponto crítico que ocorre em . Portanto, pela regra da cadeia:
Igualando à zero obtemos:
Passo 7
Sumindo com esse denominador que nunca vai poder ser zero ficamos com:
Passo 8
Agora precisamos provar que é um mínimo e que também é global. Uma alternativa é o teste da derivada segunda, a outra é simplesmente analisar o sinal da derivada . O segundo teste é mais conveniente:
Arrumando, podemos ver que o denominador não influencia no sinal. Por ser uma raiz ele é sempre positivo:
Passo 9
Podemos fazer um estudo do sinal. Precisamos saber quando a função doida é negativa ou positiva. Então vemos:
Supondo positivo podemos inverter normalmente:
Passo 10
Agora supondo negativo invertemos considerando o sinal:
Como supusemos , temos:
Portanto as desigualdades é abaixo são sempre válidas:
Logo, temos que a função doida é positiva no intervalo:
Passo 11
Portanto obtemos:
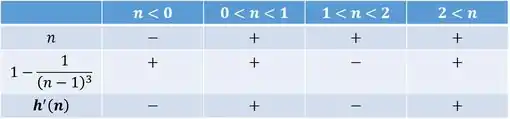
Estamos estudando o ponto . Nas redondezas de , para temos , ao passo que para temos .
Está demonstrado então que o nosso ponto é mínimo. As dimensões são então: