Uma cerca de de altura corre paralela a um edifício alto a uma distância de do edifício. Qual o comprimento da menor escada que se apoie no chão e na parede do prédio por cima da cerca?
Passo 1
Deve-se desenhar o problema e anotar as condições dadas, o que é super importante para um melhor entendimento do problema.
Ok, primeira coisa que temos que notar é que a análise desse problema começa por um corte perpendicular à extensão da cerca. Imagina como se eu tivesse olhando para cerca e para o edifício no sentido em que eles correm, como isso aqui, ó:
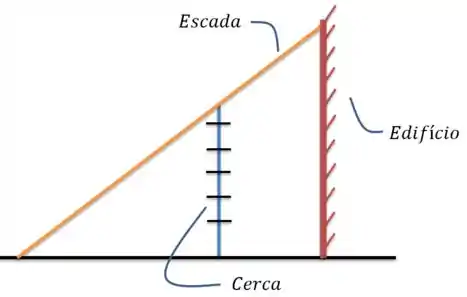
Beleza, a partir daqui já aparece um triângulo e umas distâncias relevantes para o nosso problema. Só para esclarecer tudo, a distância mínima dessa escada tem que, necessariamente, estar tocando ali no pico do arame, já que é o ponto no qual ele mais se “aproxima” do chão e da parede.
Passo 2
Temos que escrever equações que relacionam as variáveis do problema. Nesse passo, podem ser necessários conhecimentos básicos de geometria, trigonometria, etc.
O cara quer o tamanho mínimo da escada, ou seja, precisamos descrever a escada de através de alguma equação. Bom, imagina que eu chamo a distância do ponto onde ela toca o edifício de e a distância do ponto onde ela toca o chão de . Bom, por Pitágoras, eu poderia dizer que o comprimento da escada é:
Tá maneiro, e como eu chego aos valores de e de ? Nesse desenho aqui eu chamei de a distância do ponto onde a escada toca o chão até a cerca. Marquei também as distâncias que o problema me deu:
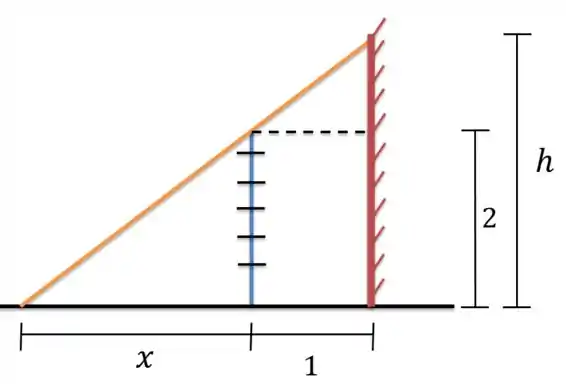
Repara, por aqui, eu tenho:
E posso matar essa altura por semelhança de triângulos, certo?
Passo 3
Analisando as equações, chegamos na função que desejamos otimizar em função de apenas uma variável.
Jogando na equação do :
Passo 4
Derivamos essa função e achamos os pontos críticos.
Vamos derivar agora, e o negócio fica assim:
Ok, como o denominador é uma raiz da soma de quadrados, será sempre positivo. Então podemos zerar só a parte de cima e ver no que vai dar:
Multiplicamos tudo por e dei uma ajeitada:
Assim, os valores de são:
Como não pode ser negativo, o ponto crítico é
Passo 5
Analisamos os sinais das derivadas antes e depois dos pontos críticos para garantir que sejam máximo ou mínimo.
Para provar que esse é ponto de mínimo, olhamos para o sinal de antes e depois do ponto. Ora, lembrando que a parte do denominador é sempre positiva, vou fazer a análise de sinal de
Essa parte corresponde ao numerador, e posso afirmar que é maior que quando e é maior enquanto . Fazendo um quadro de sinais:
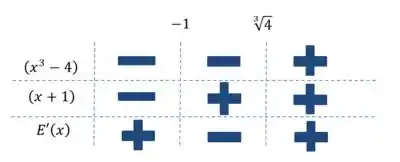
Olhando para os valores próximos a , a derivada é negativa antes e positiva depois, caracterizando um ponto de mínimo.
Passo 6
Caso achemos mais de um ponto crítico, temos que testá-los na função para ver qual deles é melhor (que dá um valor de máximo maior ou um valor de mínimo menor).
Não temos outros pontos críticos a considerar aqui.
Passo 7
Pegamos o melhor ponto crítico obtido no passo e comparamos com os valores na fronteira da função. O melhor valor de todos será o valor ótimo.
Uma da função é a escada encostada na cerca . Nesse ponto, a escada não vai encostar no prédio, então desconsideramos.
A outra fronteira é com a escada apoiada no topo da cerca, onde . Nessas condições, o comprimento da escada também tenderá a infinito.
Dessa maneira, o ponto crítico que encontramos é o ponto de mínimo global.
Para finalizar, temos que descobrir a , sendo esse o menor comprimento da escada:
Eu sei, resultado feio que dói, dá até nojo chegar num negócio assim. Mas Cálculo não é coisa de moleque, tem que ter peito e responsa para chegar nisso aqui e confiar.