Considere todos os retângulos inscritos na semi-elipse de equação , com , e que possuem um de seus lados sobre o eixo .
- Determine uma função que expresse a área destes retângulos, bem como seu domínio.
- Ache as dimensões do retângulo de maior área.
Passo 1
(a)
Bom, o primeiro passo pra matar essa questão é visualizar o problema.
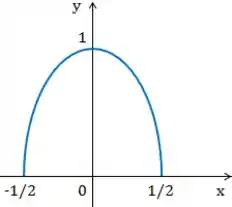
Vamos começar esboçando a semi-elipse. Vejamos onde ela cruza os eixos coordenados:
Então ela cruza o eixo em (lembrando que , por isso não temos também ).
Já pro eixo :
Beleza, a semi-elipse intercepta o eixo em e .
A partir disso, podemos tirar um esboço:
Passo 2
E ele está falando de retângulos inscritos nessa semi-elipse, com um lado sobre o eixo .
Então vão ser todos os retângulos desse tipo:
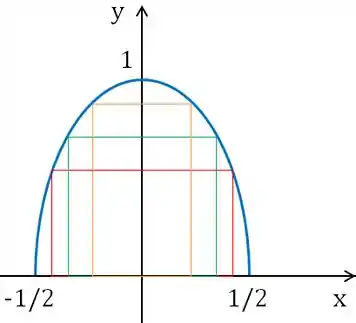
Vamos chamar os lados desses retângulos de e :
Passo 3
Beleza, agora temos que relacionar essas variáveis e . Dá uma olhada nessa figura aqui:
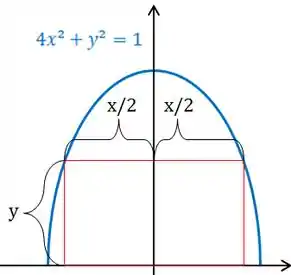
Repara aqui comigo: os pontos e estão na semi-elipse, certo? Então, usando a equação dela, vamos conseguir relacionar e !
Temos
Lembrando que , por isso .
Passo 4
Agora podemos escrever a função área!
Ela é simplesmente o produto dos lados do retângulo:
O enunciado também pediu o domínio da função, ou seja, todos os valores de para os quais ela é definida.
Definimos como sendo um dos lados do retângulo, então temos obrigatoriamente .
E apareceu uma raiz quadrada na função, o termo dentro dela não pode ser negativo
Concluímos então que o domínio de é o intervalo .
Passo 5
(b)
Queremos o retângulo de maior área, então vamos calcular o máximo global de no intervalo .
Pelas regras do produto e da cadeia:
Botando tudo no mesmo denominador:
Passo 6
Agora vamos igualar essa derivada a zero:
Pra isso dar o zero o numerador tem que ser nulo:
Passo 7
Show, então a função área tem um ponto crítico em :
Ainda não sabemos se ele é ponto de máximo ou mínimo. Então vamos calcular a área pra esse cara:
Passo 8
Pensa aqui comigo: a área dele deu . Certamente tem retângulos com área menor né? Por exemplo, se a gente pegar um retângulo bem baixinho, com um beeeem pequeno, tipo assim:
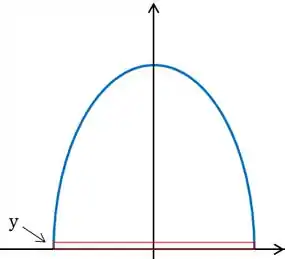
Esse pode ser tão pequeno quanto a gente quiser, então sim: há (infinitos) retângulos inscritos na semi-elipse com área menor do que .
E isso confirma que o retângulo que achamos é o de área máxima! :)
As dimensões dele são
Só uma observação: como , esse nosso retângulo é um quadrado.