Dentre todos os triângulos isósceles circunscritos a um círculo de raio existe um cuja área é máxima? E mínima? Se sim, qual é essa área? Justifique.
Passo 1
Vou começar esboçando essa situação e procurando uma fórmula para área, lembrando que uma figura circunscrita é uma figura por fora tangenciando a de dentro:
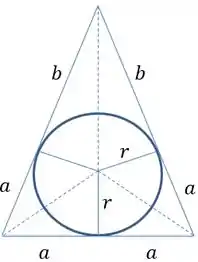
Nessa situação, eu chamei de essas distâncias do ponto de tangência no círculo até o vértice superior e de até os vértices inferiores. Por essa figura, a área total seria dada pelo seguinte, chamando os triângulos de cima de e de baixo de :
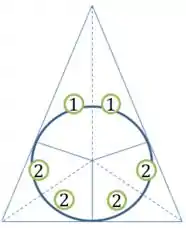
Sendo que a questão nos disse que :
A questão agora é colocar as variáveis e uma em função da outra.
Passo 2
Aí vamos usar uma semelhança de triângulos:
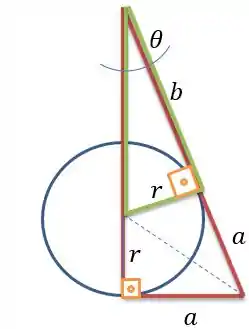
O triângulo verde e o vermelho tem dois ângulos iguais, o que faz com que mantenham a seguinte relação:
Podemos achar uma relação entre e :
Assim, a área fica:
Passo 3
Para otimizar essa função e analisar se existe máximo ou mínimo devemos derivar isso e igualar a . Vamos derivar com ajuda da Regra do Quociente e da Cadeia:
Achamos e como pontos críticos. Acontece que ao substituir nós cairíamos numa indeterminação, ou seja, esse ponto não está definido no domínio da função . Porém, se calculássemos o limite, teríamos isso:
Para chegar nesse resultado basta trabalhar L’Hospital com o segundo termo dentro do parênteses, que cairia em indeterminação. Assim, o ponto que interessa mesmo para nós é o . Ao analisar sinal de derivada antes e depois dele veríamos que ela é negativa antes e positiva depois, consistindo num ponto de mínimo da área!
Enfim, essa área mínima, que é o único ponto que achamos, será: