Um publicitário está planejando um cartaz retangular que deve ter margens de cm na parte superior e nos lados e uma margem de cm na parte inferior. Por medida de economia, a área total do cartaz deve ser a menor possível, mas a área impressa deve ter cm²: Quais devem ser as dimensões do cartaz? Justifique sua resposta!
Passo 1
Esquematizando o problema, chegamos na seguinte figura:
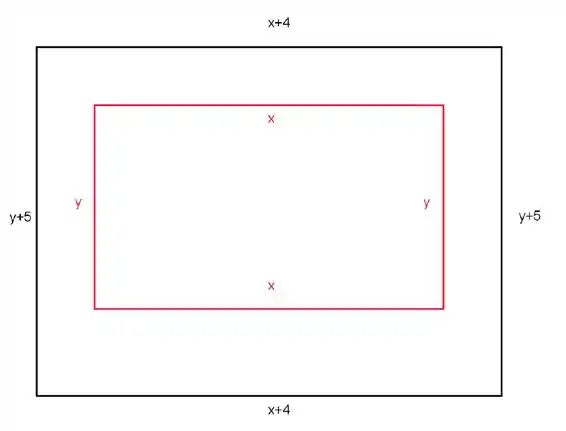
Veja que temos no retângulo maior e no menor para garantir a margem de cm nos lados e e para garantir a margem de cm em cima e cm embaixo.
Assim sendo, a área do cartaz é, multiplicando os lados do retângulo maior:
Temos, porém, duas variáveis na história. Temos que escrever uma em função da outra para poder otimizar.
Passo 2
Como faz isso? Só lembrar que a área do retângulo menor é cm² e, portanto:
Agora podemos substituir o valor de em função de :
Passo 3
Queremos achar o ponto em que essa área é mínima, para isso precisamos achar os pontos críticos que ocorrem quando a derivada é zero ou não existe. Vamos derivar então:
Temos um ponto crítico em , onde a derivada não existe. Nesse ponto, porém, a área impressa é zero, o que não nos interessa. Outros pontos críticos estão nos zeros da derivada, ou seja:
Só nos interessa a parte positiva, pois não há medida negativa.
Passo 4
Já está quase tudo certo, só precisamos mostrar que esse ponto aí é um ponto de mínimo. Para tal, é mais vantagem usar o teste da segunda derivada. Veja que:
Derivando:
No ponto :
Não precisa se preocupar com a conta. Só precisa mostrar que é positiva, pois, segunda derivada positiva no ponto crítico, pelo teste da segunda derivada, implica na presença de um ponto de mínimo, como queríamos mostrar.
Passo 5
Pelas relações dadas, temos que:
Essas são as dimensões da parte impressa. O cartaz terá: