Considere um cone circular reto de altura e raio . Dentre os cilindros circulares retos que podem ser inscritos nesse cone (conforme figura abaixo), determine a altura do cilindro que tem volume máximo.
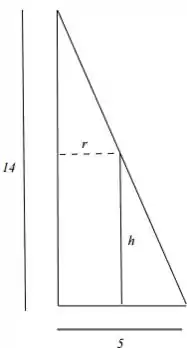
Passo 1
O volume do cilindro é dado por . Temos ainda, por semelhança de triângulos da figura acima, a seguinte relação entre e :
Assim, podemos escrever o volume em função apenas do raio do cilindro:
Derivando esse termo e igualando-o a descobriremos pontos críticos:
Repara que o vai ser um ponto de mínimo, e por isso não nos interessa. Podemos provar pela derivada primeira ou pela segunda que é ponto de máximo, mas podemos pensar assim também: dado que é ponto de mínimo e nunca podemos ter graficamente dois pontos de mínimo ou de máximo seguidos, notamos que é um ponto de máximo.
O Volume desse cilindro será dado assim:
Agora, o que o enunciado pediu foi a altura desse cilindro. Calculamos ela pela relação que tínhamos antes: