Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Pontos Críticos de Funções de Várias Variáveis

Ver Teoria
Exercício 23123456789101112131415161718192021222425262728293031323334353637383940414243444546

Enunciado

UFAM– Cálculo 2 – P1 – Questão 3

Classifique os pontos críticos da função f x , y = x 5 + y 5 - 5 x - 5 y

Passo 1

Oi, tudo bem? Essa questão parece complicada, mas vou te ajudar aqui! Temos uma função de duas variáveis

f x , y = x 5 + y 5 - 5 x - 5 y

E pediu para classificarmos os pontos críticos

Bom, para classificar esses pontos, primeiro precisamos encontrar eles, não é verdade? E como encontramos?

Em uma função de uma variável para achar os pontos críticos precisamos: derivar e igualar a zero! E para classificar fazemos o teste da derivada segunda. Isso né? Lá de cálculo 1!

Agora quando temos uma função e duas variáveis o processo é um pouco diferente (mas nem tanto!): vamos derivar e igualar a zero! Mas derivar parcialmente!

Assim teremos duas equações:

f x = 0

f y = 0

E a solução dessas duas equações nos fornecerá os pontos críticos! Agora para classificar precisamos encontrar a matriz Hessiana e aplicar em cada ponto crítico:

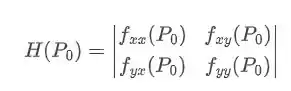
E o determinante dessa matriz aplicado no ponto, ou o hessiano, é quem vai nos ajudar a classificar os pontos, assim:

H P 0 = f x x ( P 0 ) f y y ( P 0 ) - f x y 2 ( P 0 )

Então os passos que vamos seguir são esses aqui:

  1. Derivar em x e y a função f e igualar a zero
  2. Encontrar todos os pontos críticos
  3. Derivar novamente a função f e encontrar as derivadas segundas e mistas, formar a matriz Hessiana
  4. Aplicar para cada ponto encontrado em (2) o hessiano e classificar confirme a tabela o ponto

E é isso! Mas calma, vou fazer passo a passo com você!

Passo 2

Vamos começar calculando as derivadas parciais e igualar a zero. A função é:

f x , y = x 5 + y 5 - 5 x - 5 y

Daí as parciais são:

f x = 5 x 4 - 5 = 0

f y = 5 x 4 - 5 = 0

Dessas duas equações temos:

5 x 4 = 5 → x 4 = 1 → x = ± 1

5 y 4 = 5 → y 4 = 1 → y = ± 1

Então temos 4 pontos:

P 1 1,1 ; P 2 - 1 , - 1 ; P 3 1 , - 1 ; P 4 ( - 1,1 )

Beleza até aqui?

Passo 3

Agora vamos calcular as derivadas segundas, para montar a matriz Hessiana! O determinante dessa mátria é:

H x , y = f x x f y y - f x y 2

E quando aplicamos nos pontos críticos, podemos classificá-los! Então vamos calcular as parciais duplas e a mista:

f x = 5 x 4 - 5 → f x x = 20 x 3

f y = 5 x 4 - 5 → f y y = 20 y 3

E a mista:

f x y = f y x = 0

Assim nosso hessiano fica:

H x , y = 400 x 3 y 3

Beleza?

agora #partiu aplicar nos pontos críticos!

Passo 4

Nosso hessiano é:

H x , y = 400 x 3 y 3

E os pontos críticos são

P 1 1,1 ; P 2 - 1 , - 1 ; P 3 1 , - 1 ; P 4 ( - 1,1 )

Lembrando que para classificar precisamos também do valor da derivada segunda f x x no ponto

f x x x = 20 x 3

Antes de partir para as substituições, vamos relembrar da classificação:

Agora sim, vamos olhar ponto a ponto?

  1. O ponto P 1 ( 1,1 ) :

    2. H 1,1 = 400 1 3 1 3 = 400 > 0

    f x x 1 = 20 1 3 = 20 > 0

    Então P 1 é ponto de mínimo

  2. O ponto P 2 ( - 1 , - 1 ) :

    3. H - 1 , - 1 = 400 - 1 3 - 1 3 = 400 > 0

    f x x - 1 = 20 - 1 3 = - 20 < 0

    Então P 2 é ponto de máximo

  3. O ponto P 3 ( 1 , - 1 ) :

    4. H 1 , - 1 = 400 1 3 - 1 3 = - 400 < 0

    Então P 3 é ponto de sela

  4. Por fim, o ponto P 4 ( - 1,1 ) :

H - 1,1 = 400 - 1 3 1 3 = - 400 < 0

Então P 4 é ponto de sela

Resumindo:

P 1 1,1 : m í n i m o

P 2 - 1 , - 1 : m á x i m o

P 3 1 , - 1 : s e l a

P 4 - 1,1 : s e l a

Ufa! Terminamos!

Até próxima!

Resposta

P 1 1,1 : m í n i m o

P 2 - 1 , - 1 : m á x i m o

P 3 1 , - 1 : s e l a

P 4 - 1,1 : s e l a

Exercícios de Livros Relacionados

1. Analise a natureza dos pontos críticos das seguintes funções:e) 4 y 2 e - ( x 2 + y 2 )
1-Analise a natureza dos pontos críticos das seguintes funções:c) f x ,y = x y - x 3 - y 2
2-Estude a natureza do ponto crítico das funções abaixo, mostrando que tal ponto tem a propriedade indicada.a) f x , y = x - y 4 + x + y + 2 2 , ponto de mínimo.
2- Estude a natureza do ponto crítico das funções abaixo, mostrando que tal ponto tem a propriedade indicada.b) f x , y = 1 - x 4 - y 4 , ponto de máximo.
1-Analise a natureza dos pontos críticos das seguintes funções:a) f x ,y = xs e ny