UNICAMP – Cálculo 2 – Provas antigas – P2 – 2022.1 – 3
Considere a integral dupla:
Desenhe a região de integração, e inverta a ordem da integral. Resolva a integral (você pode escolher qual integral resolver: a dada nos exercícios ou a obtida pela inversão na ordem de integração).
Passo 1
Opa meus queridos, bora pra mais uma? Aqui a coisa mais importante é sabermos qual é a região de integração. Pois quando invertemos a ordem de integração precisamos saber como vai ficar o sentido da integral (porque precisamos inverter o sentido também). Pelos limites de integração você sabe achar as retas que delimitam a área? Vem que eu te mostro. Nesse caso a região de integração é um triangulo formato pelas retas .
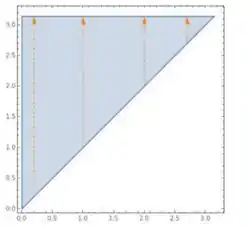
Essas setas laranjas são justamente o sentido de integração.
Passo 2
Show, bora continuar. Invertendo o sentido de integração, como a questão pede:
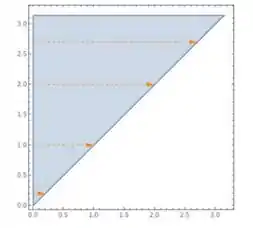
Então nossa integral fica:
Agora é só resolver a integral. Essa primeira já sai bem fácil, pois como invertemos o sentido de integração, pode ser considerada como uma “constante”, já que agora integraremos ela em . Dessa forma:
Então aquele ponto é um ponto de sela. Como nosso determinante é , então é um ponto de sela. E é isso turminha! Finalizamos por aqui 😊. Se ainda restou alguma dúvida, ou gostaria de relatar alguma coisa, manda um feedback pra gente! Vamos adorar te responder, vai se rapidinho