Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Pontos Críticos de Funções de Várias Variáveis

Ver Teoria
Exercício 44123456789101112131415161718192021222324252627282930313233343536373839404142434546

Enunciado

USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 6, Questão 2.3a

Determine os pontos críticos de f e classifique-os. Sugestão: é mais fácil não tentar usar o critério da segunda derivada.

a. f ( x ,   y )   =   x   3 y   2  

Passo 1

Eaew, belezinha?

Temos que encontrar os pontos críticos de

  f ( x ,   y )   =   x   3 y   2 .

Então, vamos encontrar os pontos críticos verificando para quais pontos ∇ f ( x ,   y )   = 0 . E como o enunciado já alertou que é mais fácil não tentar usar o critério da segunda derivada para classificar esses pontos críticos, vamos olhar para os gráficos dessas funções. Vamos analisar, por meio do gráfico, como a função se comporta perto do ponto crítico que encontramos.

Vamos lá!

Passo 2

Vamos tomar as derivadas parciais com relação a x e a y da função e igualar a zero:

∂ x f ( x , y ) = 3 x 2 y 2 = 0

∂ y f ( x , y ) = 2 x 3 y = 0

Temos os seguintes pontos críticos:

( x 0 ,   y 0 ) = ( 0 ,   λ ) ,   λ   ∈   R ;

( x 0 ,   y 0 ) = (   λ ,   0 ) ,   λ   ∈   R .

Passo 3

Vamos olhar para o gráfico dessa função:

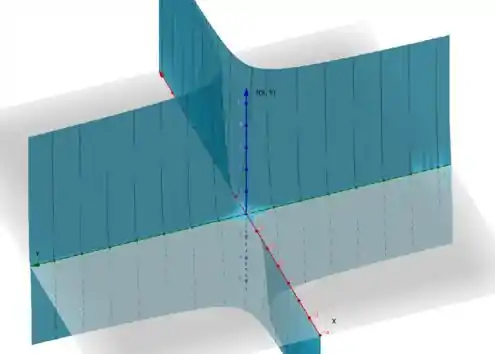
Então:

Para ( x 0 ,   y 0 ) = ( 0 ,   λ ) ,   λ   ∈   R , temos pontos de sela, ou seja, nem máximo nem mínimo;

Para ( x 0 ,   y 0 ) = (   λ ,   0 ) ,   λ > 0 , temos pontos mínimos;

Para ( x 0 ,   y 0 ) = (   λ ,   0 ) ,   λ < 0 , temos pontos máximos.

A questão foi isso! Te vejo na próxima! Tchau Tchau!

Resposta

( x 0 ,   y 0 ) = ( 0 ,   λ ) ,   λ   ∈   R , pontos de sela;

( x 0 ,   y 0 ) = (   λ ,   0 ) ,   λ > 0 , pontos mínimos;

( x 0 ,   y 0 ) = (   λ ,   0 ) ,   λ < 0 , pontos máximos.

Exercícios de Livros Relacionados

1. Analise a natureza dos pontos críticos das seguintes funções:e) 4 y 2 e - ( x 2 + y 2 )
1-Analise a natureza dos pontos críticos das seguintes funções:c) f x ,y = x y - x 3 - y 2
2-Estude a natureza do ponto crítico das funções abaixo, mostrando que tal ponto tem a propriedade indicada.a) f x , y = x - y 4 + x + y + 2 2 , ponto de mínimo.
2- Estude a natureza do ponto crítico das funções abaixo, mostrando que tal ponto tem a propriedade indicada.b) f x , y = 1 - x 4 - y 4 , ponto de máximo.
1-Analise a natureza dos pontos críticos das seguintes funções:a) f x ,y = xs e ny