UFSCAR – Cálculo 2 – Banco de Questões – Questão 41
No ponto , a função tem hessiano igual a..... Este ponto, que é crítico, é de ....
Passo 1
Oi, tudo bem? Essa questão parece complicada...
Vamos resolver juntos?
O enunciado deu uma função, um ponto e pediu o hessiano dessa função aplicado no ponto e pediu a classificação desse ponto!
Mas calma! Relembrar é viver....
o hessiano de uma função é:
Daí a classificação dessa função, quando aplicado em um ponto crítico :
Podemos ter alguns cenários:
- Se e : p é ponto de MÍNIMO local
- Se e : p é ponto de MÁXIMO local
- Se : p é ponto de SELA
- Se é inconclusivo
Sendo assim, a ideia aqui é encontrar as derivadas parciais, achar a expressão pro hessiano, aplicar no ponto e aí ver em qual classificação estamos!
Caaaaso dê inconclusivo, a gente tenta por outro caminho, mas vou te ajudar! Confia!
Vamos nessa?
Passo 2
A função é:
Começando pela derivada em :
E agora a mista:
E agora em :
Passo 3
O hessiano é:
E aplicado no ponto dado:
O teste foi inconclusivo!
Passo 4
Agora precisamos analisar a função por diferentes caminhos pra ver se é mínimo, máximo ou de sela.
Começando por fixar o em . Aí vamos analisar a função só de :
Analisando essa função temos:
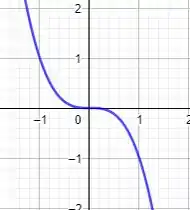
Olhando a função na outra variável, agora fixando :
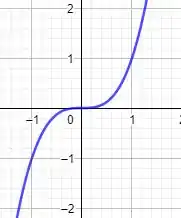
Também é um ponto de inflexão!
Então esse ponto crítico é nem de máximo, nem de mínimo! Chamamos esse ponto de degenerado!
Se olharmos nossa função em vamos ver que ela realmente, nesse ponto, não tem nem máximo, nem mínimo:
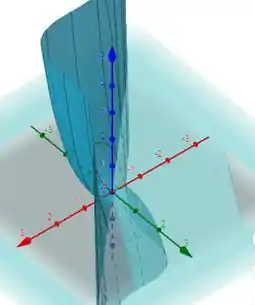beleza?
Então a resposta é: ponto degenerado.