Seja e Então, podemos afirmar que (digite onde couber, ou selecione a opção correta, dentre as opções):
No interior da região , possui exatamente ? ponto(s) crítico(s), sendo ? ponto(s) de máximo local, ? ponto(s) de mínimo local e ? ponto(s) de sela. Na fronteira da região tem-se, por multiplicadores de lagrange, ? candidatos a pontos onde ocorrem os extremos absolutos de , em . O valor mínimo absoluto da função, em , é ? e ocorre em . Já o valor máximo absoluto, em , é ? e ocorre em .
Passo 1
Oiie, tudo bem?
O enunciado nos deu a seguinte função
estabelecida sobre um domínio dado pela região Temos que encontrar os pontos críticos desta função, determinando se os mesmos são pontos de máximo ou mínimo local, ou pontos de sela. E, utilizando multiplicadores de Lagrange, identificar os candidatos a extremos absolutos da função dentro do domínio dado. Aqui, temos bastante definições para apresentar! Portanto, vamos de pouco a pouco em cada passo! Vem comigo!
Passo 2
Vamos começar pelos pontos críticos! Beleza? Os pontos críticos são aqueles que anulam o vetor gradiente da função, ou seja
em que é um ponto crítico! Ou seja, o primeiro passo é calcular as derivadas parciais da nossa função de duas variáveis! A derivada em relação a é
lembre que como temos a derivada parcial em relação a , todo é tomado como constante, e como derivadas de constantes são nulas, temos que
para as duas derivadas que sobraram, podemos usar a regra do tombo como
e, obtemos então
Podemos fazer o processo análogo para a derivada em , agora tomando como constante, para obter
ou, simplesmente
Vamos usar essas relações para obter os pontos críticos! Bora lá!
Passo 3
Lembrando que o ponto crítico é aquele em que o gradiente se anula, e portanto
Usando as derivadas que calculamos no passo anterior, temos que
O que nos dá os valores
e
ou seja, temos apenas um ponto crítico . Agora, ele é um ponto de máximo local, mínimo local, ou ponto de sela? Vamos descobrir!
Passo 4
Determinar a natureza de um ponto crítico é um trabalho de analisar o valor do determinante da matriz Hessiana, que é da forma
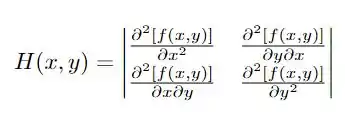
Se temos que , podemos ter um ponto de máximo ou mínimo, sob a condição
indica um ponto de mínimo, e
indica um ponto de máximo. Agoram se , temos um ponto de sela, e se , não podemos dizer nada sobre a natureza de nosso ponto crítico . Vamos calcular as derivadas de segunda ordem então!
Passo 5
Primeiro, a derivada de segunda ordem em relação a , é dada por
usando a regra do tombo, temos que a derivada é dada por
Analogamente, a segunda derivada em , é dada por
As derivadas parciais mistas são calculadas da mesma forma, e temos que
que resulta em
já que para a derivada parcial em , é uma constante, da mesma forma, temos que
Vamos usar esses resultados para calcular o determinante da nossa matriz hessiana no ponto crítico! Saca só!
Passo 6
Usando o formato da matriz hessiana que escrevemos nos passos anteriores, temos que o determinante será
usando os valores que calculamos antes, temos que
que é uma constante maior que zero. Portanto, qualquer ponto crítico obtido será um máximo ou mínimo local. No entanto, temos que
Portanto, o nosso ponto de crítico, necessariamente é um ponto de máximo local! Então, temos um ponto de máximo local, nenhum ponto de mínimo local e nenhum ponto de sela! Agora vamos analisar os multiplicadores de Lagrange e ver os extremos absolutos!
Passo 7
O método dos multiplicadores de Lagrange se trata de obter uma constante tal que
temos que é a função que queremos obter um extremo. Mas quem é ? Essa função é uma restrição! Em nosso caso, dado pela fronteira de , ou seja, temos que
Usando a definição do vetor gradiente que apresentei lá atrás! E usando a regra do tombo, temos que
Nós já obtivemos ao longo da questão o gradiente de , portanto, usando o resultado, temos que
Para que a igualdade seja verdade, precisamos que as componentes de ambos os vetores sejam iguais, temos então que
e
Agora é só resolvermos para ! Vamos lá!
Passo 8
Temos que os valores possíveis de e , são dados por
isolando , temos que
da mesma forma, para , temos que
De forma que obtemos que , portanto, usando a nossa restrição , temos que
ou, simplesmente, temos que
ou, temos os dois valores possíveis
O que nos dá dois pontos candidatos
e
Agora, qual desses pontos é o máximo e qual é o mínimo absoluto sobre a restrição? Vamos checar!
Passo 9
A nossa função é
substituindo os valores de ambos os pontos, temos que
e, temos que
Portanto, temos que é um máximo e é um mínimo! A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
A função possui ponto crítico sendo este um ponto de máximo, mas o multiplicadores de Lagrange indicam sobre a restrição dois candidatos de extremos absolutos dados por e que é um máximo e um mínimo respectivamente!