Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Método dos Coeficientes Indeterminados

Ver Teoria
Exercício 1112345678910121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768

Enunciado

Prova 1 - MAT 311 - Cálculo III – Unicamp – Questão 2

Considere a EDO:

x - 1 y ' ' - x y ' + y = x - 1 2

Note que y x = e x é uma solução da equação homogênea associada...

(a) Encontre a solução geral da equação homogênea associada a

(b) Determine a solução geral de (2).

(c) Determine a solução do PVI dado por (2), y 0 = 1 e y ' ( 0 ) = - 1 .

(d) Faça o gráfico desta solução no Mathematica. Para quais valores de x , aproximadamente, temos y ( x ) positivo?

Passo 1

Vamos começar!

Ora! A solução de uma EDO não homogênea e coeficientes constantes pode ser feita fazendo primeiro a solução da homogênea ( y h ) e depois a solução particular. A solução geral será a soma das duas.

y = y p + y h

Passo 2

a) A solução da parte homogênea é feita considerando 0 do outro lado da EDO.

x - 1 y ' ' - x y ' + y = 0

Assumindo uma solução na forma...

y = e γ x

Temos que...

x - 1 y ' ' - x y ' + y = 0

x - 1 γ 2 e γ x - x γ e γ x + e γ x = 0

x γ 2 e γ x - γ 2 e γ x - x γ e γ x + e γ x = 0

e γ x γ 2 - 1 = 0

γ 2 - 1 = 0

γ 1 = - 1 ou γ 2 = 1

Então, como temos duas raízes reais e diferentes entre si, a solução da EDO homogênea segue esse modelo aqui...

y h = c 1 e γ 1 t + c 2 e γ 2 t

y h = e x + c 1 + c 2 x

Passo 3

b) Beleza! Agora, vamos buscar uma solução particular. Para o primeiro sistema, temos que...

x - 1 y ' ' - x y ' + y = x - 1 2

Como a função que torna essa equação não homogênea é x - 1 2 . Então, a solução particular vai ter essa cara aqui...

y p x = A x 2 + B x + C

Derivando uma e duas vezes...

y p ' x = 2 A x + B

y p ' ' x = 2 A

Com essas derivadas, vamos substituir na EDO...

x - 1 y ' ' - x y ' + y = x - 1 2

x - 1 2 A - x ( 2 A x + B ) + A x 2 + B x + C = x - 1 2

2 A x - 2 A - 2 A x 2 - B x + A x 2 + B x + C = x 2 - 2 x + 1

- A x 2 + 2 A x - 2 A + C = x 2 - 2 x + 1

Obtemos assim, o seguinte sistema...

- A = 1 2 A = - 2 - 2 A + C = 1

Cujas soluções são...

A = - 1

C = - 1

Dessa forma, temos que...

y p x = - x 2 - 1

Passo 4

Agora, é a hora de resolver os PVIs.

Bem! Pro nosso sistema, a solução geral é...

y = y p + y h

y = e x + c 1 + c 2 x - x 2 - 1

c) Se liga! A gente tem que y 0 = 1 . Logo;

y 0 = e x + c 1 + c 2 x - x 2 - 1 = 1

e c 1 = 2

ln ⁡ e c 1 = ln ⁡ 2

c 1 = ln ⁡ 2

E também que y ' 0 = - 1 . Logo;

y ' ( x ) = e x + c 1 + c 2 - 2 x

y ' 0 = e ln ⁡ 2 + c 2 - 0 = - 1

c 2 = - 3

Obtemos então, que a solução do nosso sistema vai ser...

y = e x + ln ⁡ 2 - 3 x - x 2 - 1

Passo 5

d) E plotando essa função em um gráfico, obtemos que...

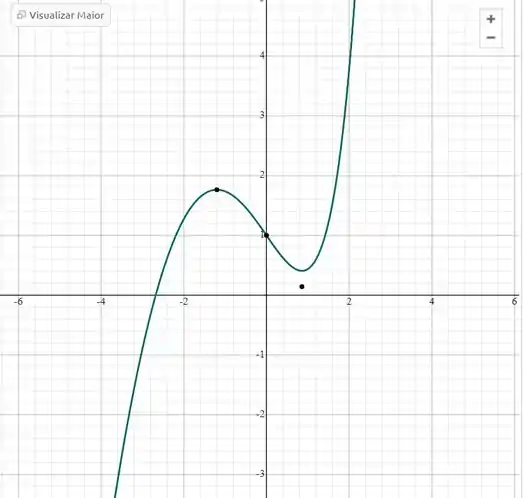
Onde pelo gráfico acima, podemos ver que pra qualquer valor de x maior que - 2,4 ; teremos um y ( x ) positivo!

Resposta

a) y h = e x + c 1 + c 2 x

b)

y = e x + c 1 + c 2 x - x 2 - 1

c)

y = e x + ln ⁡ 2 - 3 x - x 2 - 1

d)

y ≥ 2,4

Exercícios de Livros Relacionados

Resolva a equação diferencial ou problema de valor inicial usando o método dos coeficientes indeterminados. y ' ' + 9 y = e 3 x
Considere uma massa presa a uma mola sujeita a uma força de atrito ou de amortecimento. No caso de amortecimento crítico, o movimento é dado por x = c 1 e r t + c 2 t e r t . Mostre que o gráfico de x