Teste 8: Um menino utiliza um estilingue para disparar verticalmente para cima uma pedra de massa a uma velocidade inicial . A resistência do ar exerce um amortecimento do movimento proporcional à velocidade do corpo, exercendo uma força de intensidade quando a velocidade da pedra é , sendo consatante. Considerando que a aceleração da gravidade é constante e igual a , então a altura máxima atingida pela pedra é:
Passo 1
Vamos primeiro modelar o problema em si, para depois encontrar essas soluções, ok? Se desenharmos o diagrama de copo livre na pedrinha que está subindo vamos ter isso aqui:
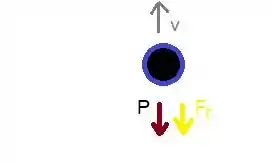
Portanto a força resultante de Newton será a soma dessas duas únicas forças atuando no objeto:
Ora a força peso é...
Enquanto eu a força de resistência do ar é...
Esse menos aí é só pra indicar que a velocidade está no sentido contrário ao sentido da força ok? Lembrando que a força Newtoniana é:
Ora, a aceleração nada mais é do que...
Enquanto que a velocidade...
Assim, ficamos com...
Dividindo todo mundo por ...
Partiu resolver essa EDO?
Passo 2
Vamos começar resolvendo a parte homogênea da EDO por comparação com a equação característica...
Ganhamos...
Então a solução da parte homogênea é...
Passo 3
Pra solução particular, pela função que torna a EDO não homogênea ser uma constante :
Normalmente chutaríamos para a solução particular uma constante também...
Mas como a solução homogênea já contém a solução constante, a gente adiciona um na constante...
Calculando as derivadas...
E substituindo na EDO...
Então a solução geral é...
Passo 4
Não resolvemos o nosso problema ainda, já que temos que encontrar a altura máxima da bolinha e não podemos fazer isso se não conhecermos quem são as constantes e . Ora, para encontrar essas constantes, vamos aplicar as condições iniciais...
A primeira condição inicial é de que no tempo a pedra não subiu nada ainda, pois o garoto nem a atirou pra cima (ainda), então...
A outra condição nos fala que no tempo a velocidade inicial é . Ora, sabemos que a derivada de representa a velocidade...
Portanto a solução do nosso problema é:
Esse nos dá a altura da pedra em cada tempo . Para encontrar a maior altura, temos que lembrar que uma função atinge o seu máximo ou mínimo local quando , então igualando a derivada a e descobrindo que tempo é esse...
Simplificando...
Colocando dos dois lados...
Esse é o tempo que a pedra atinge o máximo. A altura máxima é...
Simplificando...