Cálculo - James Stewart - Volume 2 - 7ª Edição – Capítulo 14 – Seção 5 – Exercício 37
(Capítulo 14.5 – Exercício 37) A velocidade da propagação do som através do oceano com salinidade de 35 partes por milhar foi modelada pela equação
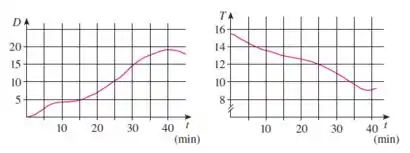
onde C é a velocidade do som (em metros por segundo), T é a temperatura (em graus Celsius) e D é a profundidade abaixo do nível do mar (em metros). Um mergulhador começa um mergulho tranquilo nas águas oceânicas, e a profundidade do mergulho e a temperatura da água ao redor são registradas nos gráficos a seguir. Estime a taxa de variação (em relação ao tempo) da velocidade do som através do oceano experimentada pelo mergulhador 20 minutos depois do início do mergulho. Quais são as unidades?
Passo 1
Salveee pessoal! Se liga só, nessa questão temos essa função:
E aí queremos estimar a taxa de variação da velocidade do som após 20 minutos depois do início do mergulho. Isso significa determinar quando , sendo necessário utilizar a regra da cadeia, já que é uma função que depende de (temperatura) e de (profundidade abaixo do nível do mar).
Então vamos lá??
Passo 2
Como queremos a derivada de em relação ao tempo, sabendo que , vamos ter pela regra da cadeia:
=
Showw, então derivando em relação a e a , temos
Passo 3
Observando o gráfico, temos que quando , a temperatura é e
Além disso, estimando os valores de e utilizando :
Showww, então podemos calcular após 20 minutos.
E é isssoooo