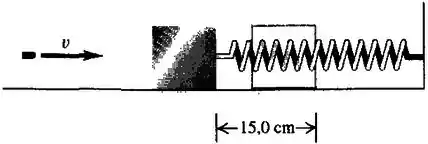
Uma bala de disparada por um rifle penetra e fica retida em um bloco de ligado a uma mola e apoiado sobre uma superfície horizontal sem atrito. O impacto produz uma compressão de na mola. A calibração mostra que uma força de comprime a mola . Calcule o módulo da velocidade do bloco imediatamente após o impacto. Qual era a velocidade inicial da bala?
Passo 1
Temos uma colisão acontecendo, assim a primeira coisa a saber é que o momento linear do sistema é constante.
Ele não define a colisão, mas diz que as esferas ficam coladas, então depois da colisão todas tem a mesma velocidade, isso é o mesmo que falar que a colisão é inelástica.
Passo 2
Após o impacto, não vamos ter forças dissipativas, como o atrito, atuando. Isso nós diz que a energia mecânica do sistema DEPOIS da colisão é constante.
Beleza agora a energia final
A compressão da mola foi de , assim
Repara que se igualarmos não vamos resolver nada porque temos duas incógnitas.
Passo 3
O enunciado nos diz que a calibração para comprime a mola , então
Agora temos a energia mecânica final
Passo 4
Sabemos agora que
Igualando as energias
Passo 5
Vamos agora usar a conservação do momento linear, como estamos trabalhando com uma dimensão não precisamos escrever vetorialmente.
Substituindo os valores dados e a velocidade final do conjunto que acabamos de encontrar, temos
Resposta