Dois pêndulos de igual comprimento estão situados inicialmente como na figura. O pêndulo da esquerda é solto da altura e colide contra o outro, que estava inicialmente em repouso. Nesta colisão vamos desprezar a massa dos fios e quaisquer efeitos de atrito.

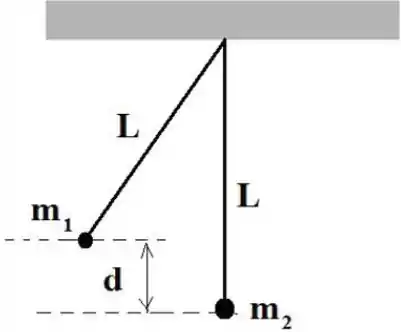
Suponha primeiramente que a colisão é elástica.

a) Escreva as equações das leis de conservação que caracterizam a colisão em si, relacionando as quantidades relevantes logo antes e logo depois da colisão.

b) Seja o caso particular em que . Encontre a altura que se eleva o corpo . (Faça os cálculos, não use respostas prontas!)

Agora suponha que a colisão é totalmente inelástica.

c) Se , a que altura se eleva o centro de massa do conjunto após a colisão?

Nessa questão também supomos que a colisão é elástica. Então também há conservação da energia cinética total:

b)

Há 3 etapas nesse movimento:

1. Queda de até colidir com
2. Colisão elástica de com
3. Subida de depois da colisão

Vamos ver o que acontece em cada uma delas!

Etapa 1: Queda de

• é solto do repouso, logo sua energia cinética é
• é solto de de uma altura em relação a . Vamos considerar a altura de como o zero de energia potencial. Assim, a energia potencial gravitacional de é

Mas ao longo da queda, a energia potencial se transforma em energia cinética, até que logo antes da colisão, chega na mesma altura de e temos

Como não há atrito ou forças não-conservativas, pela conservação da energia mecânica, logo antes da colisão toda energia potencial se transformou em energia cinética, logo

E temos

Portanto:

A gente sabe que mas vamos deixar por enquanto e no final das contas a gente substitui, beleza?

Etapa 2: Colisão

está em repouso logo antes da colisão, ou seja .

Pra gente achar até que altura vai subir, temos que achar . Então vamos aplicar a conservação do momento linear total! Já vimos antes que

Mas nessa questão . Então substituindo os valores que já temos:

Agora vamos aplicar a conservação da energia cinética:

Lembrando que , então

Show! Obtivemos o sistema

Substituindo a primeira equação na segunda, obtemos:

Vamos supor que vai mexer depois da colisão, ou seja que , então:

Portanto, nessa questão, temos

Etapa 3: Subida de pós-colisão

Agora vai acontecer o inverso do que aconteceu pra na etapa 1: a energia cinética vai ser completamente transformada em energia potencial gravitacional até atingir a altura que procuramos.

Logo depois da colisão, a energia cinética de é:

E quando o corpo atinge a altura , sua energia potencial é:

Portanto,

Opa! Achamos antes ! Então

sobe a uma altura de .

c)

Nessa questão e a colisão é totalmente inelástica, então os corpos vão sair grudados, formando um só corpo de massa . E, logicamente, é a mesma pra e .

Novamente temos 3 etapas no movimento:

1. Queda de até colidir com
2. Colisão totalmente inelástica de com
3. Subida de depois da colisão

Vamos ver o que acontece em cada uma delas!

Etapa 1: Queda de

Cara, essa etapa vai ser idêntica à etapa 1 da colisão elástica. Pra essa etapa a natureza da colisão não faz diferença (ela ainda não aconteceu!), então da mesma forma vamos obter

Etapa 2: Colisão totalmente inelástica

Não podemos aplicar a conservação da energia cinética, mas fica tranquilo que pra conservação do momento linear total não tem problema:

E como :

Etapa 3: Subida do conjunto após a colisão

O corpo sai da colisão com uma energia cinética

e no fim do movimento, chegando numa altura que queremos achar, sua energia potencial gravitacional é

E depois da colisão, podemos aplicar a conservação da energia mecânica sem problemas, ou seja:

Substituindo :

Então o centro de massa do conjunto se eleva de aproximadamente após a colisão :)