7. Um projétil de é disparado horizontalmente com uma rapidez de contra um bloco de madeira de . O bloco de madeira se encontra em repouso. Após a colisão, o projétil fica incrustado no bloco de madeira. Sabendo que o coeficiente de atrito cinético entre o bloco e o solo é de , determine a distância aproximada percorrida pelo bloco após a colisão.
Passo 1
Olá, galerinha! Aqui nós temos uma questão de conversação do momento, onde temos um projétil atingindo um bloco e depois dessa colisão há um deslocamento do bloco com o projetil. O antes e depois ficam assim:
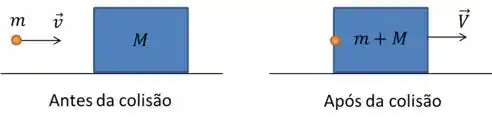
O problema nos forneceu os dados da massa do projetil, massa do bloco e velocidade do projetil. Então agora temos que descobrir com qual velocidade o bloco sai após a colisão. Daí a gente consegue depois calcular a distância percorrida pelo bloco.
Bora lá!
Passo 2
Pela conservação do momento, temos que
Substituindo,
Isolando
Agora vamos calcular a distancia percorrida pelo bloco!
Passo 3
Acabamos de calcular a velocidade inicial do bloco e como queremos saber o deslocamento dele, temos que velocidade final será zero (que é quando ele para).
Para calcular a distância, vamos usar
Onde, é a aceleração. Que neste caso será dada por,
Com isso, ficamos com
Substituindo os valores,
Isolando ,
Prontinho!
Resposta
Letra B