Um carro parte do repouso com aceleração constante de módulo e após percorrer uma certa distância, ele colide com um caminhão. Imediatamente antes de colidirem, o carro e caminhão tinham velocidades de mesmo módulo em direções perpendiculares e, após a colisão eles passam a se movimentar juntos. Sabendo que caminhão tem uma massa cinco vezes maior do que a do carro, responda as perguntas abaixo.
a) Qual a distância percorrida pelo carro desde o instante em que parte do repouso até aquele em que colide com o caminhão?
b) Qual o módulo da velocidade do sistema carro-caminhão imediatamente após a colisão?
c) Qual é o trabalho realizado pelas forças internas do sistema carro-caminhão durante a colisão?
Passo 1
Na letra (a), queremos a distância que o carro anda antes da colisão.
O carro sofre uma aceleração constante, então, ele vai realizar um movimento uniformemente variado.
Assim, podemos usar as equações de MUV para encontrar a distância percorrida:
Passo 2
Beleza! como não temos o tempo que durou o movimento, é mais prático utilizar direto a equação de Torricelli:
OBS: Escrevi as velocidades como e para não confundir com o valor no enunciado.
Mas, também podemos usar as duas primeiras para encontrar a distância. Basta isolar na segunda e substituir na primeira... isso é de onde surge a equação de Torricelli hahah.
Enfim, continuando... sabemos que o carro parte do repouso, então sua velocidade inicial é nula. Além disso, a velocidade final será (velocidade com que o carro chega na colisão):
Passo 3
Na letra (b), queremos o módulo da velocidade do conjunto (carro-caminhão) após a colisão.
O enunciado diz que o carro e o caminhão tem suas velocidades com mesmo módulo em direções perpendiculares, então temos uma colisão bidimensional.
Vamos definir as direções:
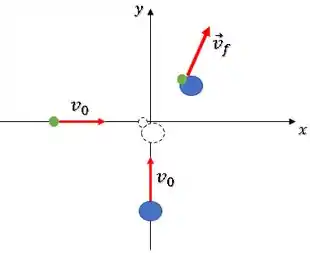
Mas como fazemos para encontrar a velocidade final ?
As únicas forças que atuam na direção do plano durante a colisão são as forças que os veículos exercem entre si (forças internas), logo se anulam.
Já as forças externas, como a peso e normal, também se anulam, logo, não há nenhuma força resultante externa atuando no sistema.
Assim, temos que o momento linear se conserva:
Passo 4
Vamos usar a forma vetorial direto para achar o nosso resultado.
O momento linear inicial será a soma dos momentos lineares do carro e do caminhão:
Podemos dizer que o carro tem uma massa , logo o caminhão terá uma massa (5 vezes maior):
Cortando :
Passo 5
Agora, podemos encontrar o módulo da velocidade com:
Assim, achamos que:
Podemos tirar da da raiz para ficar mais bonitinho:
Lembrando que aqui não colocamos a unidade, pois a unidade está dentro de .
Passo 6
Na letra (c), queremos o trabalho das forças internas.
Como essas forças internas não são muito bem definidas, queremos na verdade apenas o valor em módulo desse trabalho.
Então, vamos aplicar o teorema trabalho-energia cinética e depois responder com o valor resultante em módulo:
A energia cinética inicial é a soma das energias cinéticas do carro com o caminhão:
Enquanto a energia cinética final será a energia cinética do conjunto (carro-caminhão):
Passo 7
Então o trabalho será:
Esse trabalho é negativo por que teve energia cinética dissipada na colisão. Essa energia se perde como calor, som, rachaduras e amassados nos veículos, etc.
Resposta
(a)
(b)
(c)