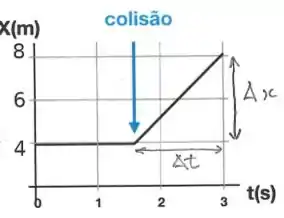
10. Duas bolas de mesmo massa sofrem uma colisão. A colisão é unidimensional. A bola tem rapidez inicial e colide com a bola em repouso. O gráfico da posição em função do tempo da bola é mostrado abaixo. A seta azul marca o instante da colisão ().
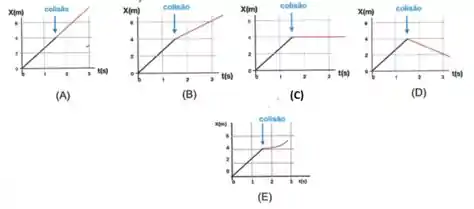
Qual das opções representa corretamente a posição em função do tempo para a bola ?
Passo 1
Olá, pessoal! Tudo bom? Aqui nós temos nós temos uma questão de conservação do momento. Ou seja, o momento antes da colisão tem que ser igual ao depois da colisão.
Então uma forma de descobrir qual gráfico representa a bola após a colisão é comparando das velocidades de antes e depois, já que as massas são iguais.
Bora lá!
Passo 2
Pelo gráfico fornecido no problema, temos que a velocidade da bola após a colisão é dada por,
Agora vamos comparar com a velocidade da bola antes da colisão. Repara que todos os gráficos indicam a mesma velocidade, dada por
Opaaaa! Repara que as velocidades de antes e depois foram iguais. Ou seja, pela conservação do momento temos que após a colisão a bola ficou em repouso e a bola saiu com a velocidade inicial da bola .
Com isso, temos que o gráfico que não apresenta mudança de velocidade da bola após a colisão é o gráfico C.
Fim!
Resposta
Letra C