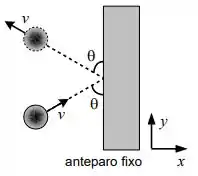
Uma bola de borracha de massa desliza sobre uma superfície horizontal sem atrito e colide com um anteparo fixo. O módulo da velocidade da bola é . A colisão faz um ângulo com a face do anteparo como ilustra a figura. A bola é refletida a mesma velocidade escalar e com o mesmo ângulo. O contato entre a bola e o anteparo dura . Utilize o sistema de coordenadas indicado.
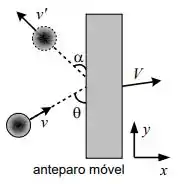
c) Suponha agora uma nova colisão, com a bola tendo a mesma velocidade inicial de módulo e ângulo com a face do anteparo. Mas agora o anteparo pode se mover livremente e sua massa é dada por . Sabendo que o módulo da velocidade da bola refletida é imediatamente depois da colisão e que ela faz um ângulo com o anteparo, calcule a velocidade do anteparo. Determine se a colisão foi elástica ou inelástica.
Passo 1
Agora, nosso sistema será a bolinha mais o anteparo. Ou seja, as forças tanto da bolinha no anteparo quanto do anteparo na bolinha são forças internas e se anulam.
Temos um sistema isolado e podemos dizer que o momento linear se conserva:
Passo 2
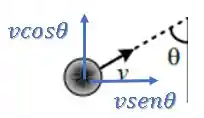
Vamos decompor a velocidade inicial:
Passo 3
Vamos decompor as duas velocidades finais.
A da partícula:
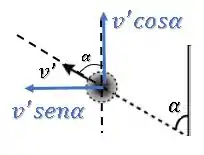
A velocidade do anteparo não conhecemos nem a direção nem o módulo, então vamos mantê-lo como um vetor desconhecido:
Passo 4
Voltando à conservação, temos:
O ângulo e :
Por último, podemos substituir as massas:
Passo 5
Agora, vamos calcular as energias cinéticas antes e depois da colisão e ver se a energia cinética do sistema se conserva ou não.
Inicialmente, temos apenas a energia cinética da partícula:
No final, temos a energia cinética da partícula mais a do anteparo:
Já sabemos o valor de , mas ainda falta acharmos o módulo da velocidade do anteparo :
Já vamos deixar esse valor elevado ao quadrado pois é disso que precisamos para o cálculo da energia cinética mesmo.
Como a energia cinética final é diferente da energia cinética inicial:
A energia cinética do sistema não se conserva e temos uma colisão inelástica.
Resposta
Colisão inelástica