Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Colisões Inelásticas

Ver Teoria
Exercício 82123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081838485868788899091

Enunciado

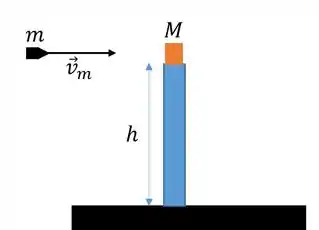
Uma bala de massa m e velocidade v m é disparada contra um bloco de massa M , que inicialmente se encontra em repouso na borda de um poste de altura h , conforme mostra a figura abaixo. A bala aloja-se no bloco que, devido ao impacto, cai no solo. Sendo g a aceleração da gravidade, e não havendo atrito nem resistência de qualquer natureza, calcule o módulo da velocidade com que o conjunto atinge o solo

a) v = m v 0 M + m 2 - g h 2

b) v = m v 0 M + m 2 - g h

c) v = m v 0 M + m 2 + 2 g h

d) v = m v 0 M + m + 2 g h

e) v = m v 0 M + m 2 - 2 g h

Passo 1

Como a bala se aloja no bloco, temos uma colisão totalmente inelástica, onde o sistema sai com uma velocidade v x horizontal. Pela conservação de momento linear

m v m + M 0 = M + m v x

v x = m v m M + m

Como a aceleração da gravidade atua na direção vertical a velocidade horizontal desse sistema não é alterada. Agora vamos ver a velocidade vertical

Passo 2

No começo da queda, a velocidade vertical inicial é nula. A velocidade vertical no momento em que o sistema encosta no solo, v y , pode ser obtida pela equação de Torricelli

v y 2 = 0 2 + 2 g h

v y = 2 g h

Passo 3

O vetor velocidade é dado por

v → = v x i ^ + v y j ^ = m v m M + m i ^ + 2 g h j ^

O módulo da velocidade é dada por

v = v x 2 + v y 2

v = m v 0 M + m 2 + 2 g h

Resposta

(C)

Exercícios de Livros Relacionados

Na Fig. 9-63, o bloco 1 (com uma massa de 2,0k g ) está se movendo para a direita com uma velocidade escalar de 10m / s e o bloco 2 (com uma massa de 5,0k g ) está se movendo para a direita com uma ve
Uma colisão frontal perfeitamente inelástica ocorre entre duas bolas de massa de modelar que se movem ao longo de um eixo vertical. Imediatamente antes da colisão, uma das bolas, de massa 3,00k g , es
Um vagão fechado em um pátio de manobras é colocado em movimento no topo de um morro artificial. O vagão desce silenciosamente e sem atrito sobre um trilho horizontal reto, onde se acopla com um vagão
Uma bala de 10,0g é disparada e entra em um bloco de madeira de 200g em repouso sobre uma superfície horizontal. Após o impacto, o bloco desliza 8,00m antes de parar. Se o coeficiente de atrito entre
Duas lontras brincalhonas deslizam ao encontro uma da outra sobre uma superfície horizontal lamacenta (e, portanto, sem atrito). Uma delas, com massa de 7,50k g , desliza da direita para a esquerda a