Q - Considere uma bala disparada horizontalmente contra dois blocos inicialmente em repouso sobre uma superfície sem atrito. A bala atravessa o bloco e fica alojada no bloco . A velocidade final do bloco é e do bloco é . Desprezando o material removido do bloco pela bala e a resistência do ar e considerando que ; ; ;
calcule a velocidade da bala ao entrar no bloco ;
calcule a velocidade da bala ao entrar no bloco ;
faça o gráfico de da colisão entre a bala e o bloco ;
faça o gráfico de da colisão entre a bala e o bloco .
Passo 1
Vem comigo que a gente detona com esse problema!
O que temos que usar nesse problema é a conservação do momento linear em tudo kkk.
Podemos encontrar a velocidade da bala ao entrar no bloco , considerando o momento inicial como sendo antes da colisão e momento final como sendo depois da colisão quando a bala está alojada no bloco .
Para encontrar a velocidade da bala ao entrar no bloco , vamos lembrar que essa velocidade é igual a velocidade com que a bala sai do bloco .
Então podemos usar a conservação de momento linear, onde o momento inicial é antes da colisão da bala com o bloco e o momento final quando a bala acaba de sair do bloco .
Depois de encontrarmos essas velocidades podemos achar os valores dos momentos da bala e dos blocos e montar os gráficos pedidos em e em .
Mãos à obra então!
Passo 2
Começando com o item .
Na situação que comentamos no passo , temos o seguinte da conservação de momento:
O segundo termo do lado esquerdo vem do fato da bola e o bloco dois andarem juntos. Agora vamos isolar que é a velocidade que queremos saber.
Substituindo os valores que conhecemos, temos:
Com isso temos que:
Passo 3
Agora vamos para o item .
Vamos usar a conservação do momento agora para a situação que vimos no passo , assim temos:
O que queremos encontrar é , então vamos isolá-lo, assim:
Substituindo com os valores que conhecemos, temos:
Com isso temos que:
Passo 4
Agora vamos para cima do item .
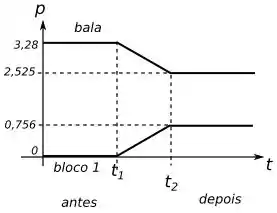
Para montar o gráfico da colisão da bala com o bloco , temos que saber o momento inicial e final da bala e do bloco .
O momento inicial e final da bala respectivamente é:
O momento inicial e final do bloco respectivamente é:
Com isso o gráfico fica da seguinte forma:
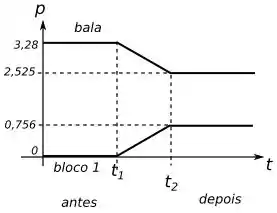
Passo 5
Agora vamos atrás do gráfico pedido em .
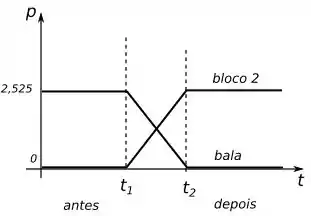
Para montar o gráfico da colisão da bala com o bloco , temos que saber o momento inicial e final da bala e do bloco . O momento inicial da bala nesse caso vai ser igual ao momento dela depois que sai do bloco .
Então o momento inicial e final da bala respectivamente é:
O momento inicial e final do bloco respectivamente é:
Com isso o gráfico fica da seguinte forma:
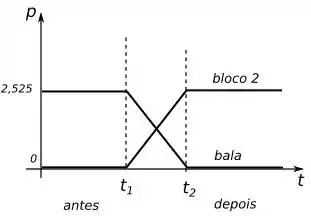
Resposta