Um bloco sobre um piso horizontal pode estar inicialmente: em repouso, em movimento no sentido positivo do eixo ou em movimento no sentido negativo do mesmo eixo. O bloco explode em dois pedaços que continuam a se mover ao longo do eixo . Suponha que o bloco e os dois pedaços formem um sistema fechado e isolado. A figura mostra seis possibilidades para o gráfico dos momentos do bloco e dos pedaços em função do tempo . Pode-se dizer que:
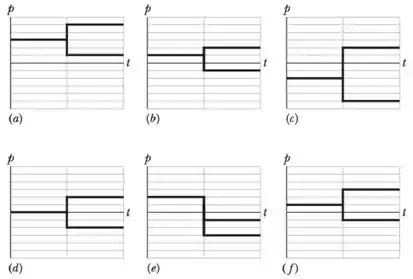
(a) As situações , , , são físicamente impossíveis.
(b) Todas as situações são físicamente impossíveis.
(c) As situações , , , são físicamente impossíveis.
(d) As situações , , , são físicamente impossíveis.
(e) Todas as situações são físicamente possíveis.
Passo 1
Temos um bloco em um sistema isolado que se parte em dois fragmentos.
O que ele quer dizer com um sistema isolado?
Bom, isso quer dizer que não há a ação de forças externas no sistema.
E lembra que quando isso acontece, o momento linear do sistema se conserva?
Pronto, tá aí a nossa relação!
Agora, basta a gente ver se o momento linear inicial do bloco é igual a soma dos momentos lineares dos dois fragmentos.
Passo 2
Começando com a letra (a):
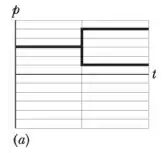
Vamos chamar daqui em diante de cada unidadezinha do gráfico...
Então, inicialmente temos:
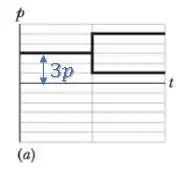
Já no final, temos:
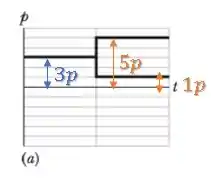
Logo, o momento linear do sistema não se conservou:
Assim, a situação é impossível.
Passo 3
Vamos fazer o mesmo procedimento para as outras situações.
Situação :
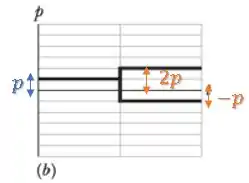
Como o momento linear se conserva:
A situação é possível.
Situação :
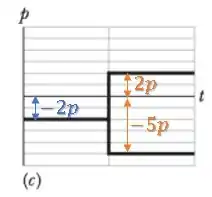
Como o momento linear não se conserva:
A situação é impossível.
Situação :
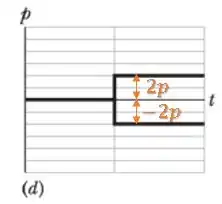
Como o momento linear se conserva:
A situação é possível.
Situação :
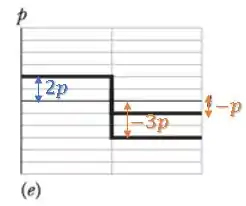
Como o momento linear não se conserva:
A situação é impossível.
Situação :
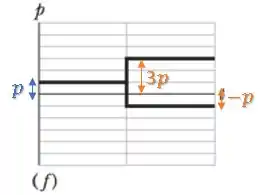
Como o momento linear não se conserva:
A situação é impossível.
Passo 4
Vimos que as situações , , , são impossíveis.
Ficamos com a letra (c).
Resposta
Letra (c)