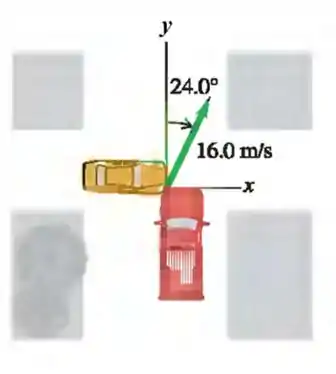
A figura mostra dois veículos que colidem de modo totalmente inelástico num cruzamento . A velocidade dos escombros conjuntos tem valor imediatamente após a colisão e direção que faz com o eixo . O veículo , que vinha no eixo da figura, tem massa , e o veículo tem massa . Considere o sistema isolado durante a colisão.
Forneça o vetor momento do centro de massa do sistema imediatamente depois da colisão, , e imediatamente antes da colisão, . Justifique.
Qual a velocidade escalar de cada veículo antes da colisão?
Forneça o vetor força que atuou sobre o veículo , , sabendo que a colisão teve duraçãoo de .
Passo 1
Quando estamos lidando com uma colisão totalmente inelástica, devemos lembrar que nesse tipo de colisão, os objetos envolvidos tem a mesma velocidade final, ou seja, eles saem juntos.
Para calcular o vetor momento dos corpos depois da colisão, devemos primeiro lembrar da sua definição:
Depois da colisão, pelo fato de os carros terem a mesma velocidade, temos:
Para determinar o vetor momento em relação aos eixos, vamos decompor ele em suas componentes e .
Em , temos:
Substituindo os valores, temos:
Em , temos:
Substituindo os valores, temos:
Portanto, o vetor momento depois da colisão é:
Por se tratar de um sistema isolado, onde forças externas não estão atuando, podemos aplicar a conservação do momento linear, desse modo o vetor momento do sistema antes da colisão será igual ao vetor momento linear depois da colisão:
Passo 2
Pelo fato de os carros estarem posicionados conforme mostra a figura, percebemos, que antes da colisão, a componente do vetor momento linear é devida exclusivamente ao veículo , que vinha no eixo . Analogamente a componente do vetor momento linear é devida exclusivamente ao veículo , que vinha no eixo . Com isso em mente, temos:
Para o veículo :
Substituindo os valores, temos:
Para o veículo :
Substituindo os valores, temos:
Passo 3
Para determinar a força que atuou sobre o veículo , precisamos lembrar do teorema Força-Impulso, ele nos diz:
Como temos a velocidade do veículo antes e depois da colisão , podemos achar a força, se liga!
Substituindo os valores, temos:
Veja que estamos decompondo a velocidade final, pois queremos descobrir o vetor força, e a melhor maneira é determinar as componentes em separado.
Resposta
;