A figura mostra o resultado de uma colisão entre dois corpos de massas desiguais. Determine:
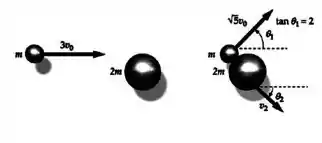
O ângulo
A rapidez da maior massa após a colisão.
Classifique a colisão quanto à variação de energia cinética, justificando sua resposta.
Passo 1
Antes de determinar o ângulo , vamos calcular o valor do seno e do cosseno de , temos que:
elevando ao quadrado e substituindo , temos:
Logo, temos que:
Agora sim podemos determinar , para isso vamos usar a conservação de momento linear, uma vez que não atuam forças externas ao sistema:
Em , temos:
Cortando e substituindo o valor do cosseno de , temos:
Em , temos:
Dividindo por , temos:
Passo 2
Agora que sabemos o valor de , basta substituir em uma das equações achadas, se liga:
Passo 3
Para determinar o tipo de colisão, vamos analisar a variação da energia cinética:
Para a energia cinética inicial, temos:
Para a energia cinética final, temos:
Ou seja:
Por conta de a energia cinética se conservar, temos que a colisão é dita perfeitamente elástica.
Resposta