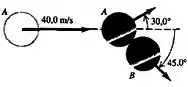
Um disco de hóquei está em repouso sobre uma superfície lisa de gelo quando é atingido por outro disco de hóquei que estava inicialmente se movendo a e que passa a se mover sofrendo um desvio de da sua direção original. O disco de hóquei passa a se mover com velocidade formando um ângulo de com a direção original de . As massas dos discos são iguais. Calcule o módulo da velocidadede cada disco de hóquei depois da colisão. Qual a fração da energia cinética inicial do disco de hóquei A que foi dissipada durante a colisão?
Passo 1
Temos uma colisão acontecendo, assim a primeira coisa a saber é que o momento linear do sistema é constante.
Como o disco está em repouso temos
Passo 2
Vamos começar escrevendo as velocidades iniciais dos dois discos.
Passo 3
Precisamos agora escrever as velocidades depois da colisão, como não sabemos o módulo das velocidades vamos chamá-los de e . Vamos precisar também usar a “regra do COlado/SEparado”. Para a velocidade de
Primeiro par ao eixo
E agora para o eixo
Escrevendo ela vetorialmente
Passo 4
Vamos fazer a mesma coisa com a velocidade de
Primeiro par ao eixo
E agora para o eixo
Escrevendo ela vetorialmente
Passo 5
Como as massas são iguais vamos chama-las de . Pela colisão vamos ter
Vamos ter
Passo 6
Para isso vamos ter o sistema
Pela segunda equação
Vamos substituir na primeira
Então
Passo 7
Vamos fazer a variação de energia cinética do sistema para descobrir isso
Repara que temos aquela massa perdida ali, mas ele quer a fração da energia cinética que foi dissipada, então precisamos do quanto foi dissipado e vamos dividir pela energia cinética inicial.
Eu usei o a variação de energia cinética sem sinal porque já sabemos que houve perda, ele só quer a fração então o sinal não importa.
Ele perdeu da energia cinética.
Resposta
Ele perdeu da energia cinética.