Um bloco , com massa , está inicialmente em repouso, comprimindo de uma mola de constante elástica . Após ser liberado, o bloco se desprende da mola com velocidade , dirigindo-se a outro bloco idêntico (bloco ) situado mais à frente na mesma superfície horizontal sem atrito. O bloco está inicialmente parado. Depois da colisão frontal entre os dois blocos, eles saem unidos com velocidade . Mais adiante, o conjunto dos dois blocos colide elasticamente com uma esfera de massa , inicialmente em repouso, que está conectada a um fio ideal de comprimento Considere .
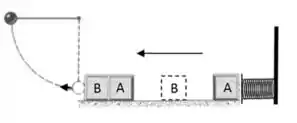
(a) Determine .
(b) Determine a perda relativa de energia cinética na colisão entre e .
Supondo que , determine:
(c) o comprimento do fio para que, como consequência da colisão sofrida pela esfera, o fio descreva um arco de exatamente , conforme a figura.
Passo 1
a)
O bloco A parte do repouso e anda na superfície horizontal se atrito. Até que ele colide com o bloco B.
Nessa etapa em que ele tá andando, antes da colisão, temos que a energia mecânica se conserva, pois não há força dissipativa atuando (atrito entre a superfície e o bloco).
Então
No inicio, ele tá comprimindo a mola em , mas parte do repouso, então . Antes da colisão ele só tem energia cinética mesmo.
Note que passei a compressão da mola para metro.
Resolvendo isso:
Beleza! Então essa é a velocidade com que o bloco A chega para colidir inelásticamente com o B. Bom, durante a colisão o momento linear se conserva, então
Nesse tipo de colisão os blocos saem juntos, então a velocidade final deles é a mesma, Além disso o bloco B tá inicialmente em repouso, então a velocidade inicial dele é zero. Assim,
O enunciado fala que os blocos são idênticos, então .
Então
Show?!
Passo 2
b)
Agora queremos saber a perda de energia cinética relativa na colisão:
Antes da colisão, só o A se movia, então
Depois da colisão, ambos os blocos se movem, com mesma velocidade .
Então o .
Então
Prontinho!
Passo 3
c)
Nessa etapa, os dois bloquinhos vão colidir elasticamente com a esfera, e ela vai subir. A energia mecânica se conserva, então a energia cinética dos blocos será transformada em energia potencial gravitacional para a bolinha.
Dessa forma
Show?
Resposta
a)
b)
c)