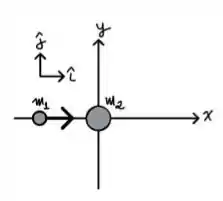
Duas partículas podem deslocar-se sem atrito sobre um plano horizontal , com vetores unitários e na direção dos eixos e positivos, respectivamente. A partícula , de massa , inicialmente desloca-se com velocidade ao longo do eixo .
Ela então se choca com a partícula , de massa , que estava inicialmente parada na origem do sistema de coordenadas (vide figura). Após o choque, sai com velocidade .
(a) Calcule, em termos dos vetores unitários e , a velocidade de após o choque, explicitando a(s) grandeza(s) conservada(s). Justifique sua resposta.
(b) Calcule a variação da energia cinética que ocorreu devido ao choque.
(c) Calcule, em termos dos vetores unitários e , o vetor-posição do centro de massa do sistema segundos após o choque.
Passo 1
a) Como não há forças externas, o momento linear do sistema se conserva.
Portanto, substituindo os valores:
Passo 2
b)
Passo 3
c) Como , também se conserva.
Cinco segundos após o choque(que ocorre na origem), o vetor posição do centro de massa será:
Resposta
a)
b)
c)