Dois asteroides, um de massa e outro de massa , estão se movendo no espaço, como mostra a figura. Os asteroides colidem no ponto e a colisão é perfeitamente inelástica. Qual é o ângulo que a velocidade do objeto único resultante da colisão faz com o eixo ?
(a)
(b)
(c)
(d)
(e)
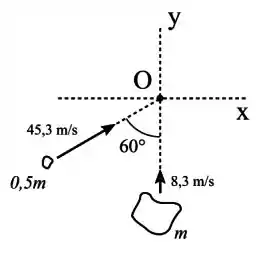
Passo 1
Como a colisão é totalmente inelástica, temos que os dois asteroides seguem juntos após colidirem. Pela conservação de momento temos
O momento inicial é o momento dos dois asteroides de massas e , assim
A velocidade pela figura é
E a velocidade é dada por
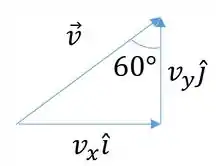
Assim
Passo 2
O momento final é dado por
Igualando os momentos final e inicial
Cortando as massas
Organizando
Passo 3
Pra saber que ângulo esse vetor faz com o eixo , podemos olhar as componentes de
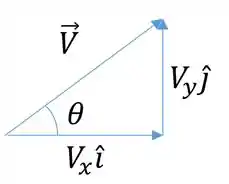
Olhando pra esse triângulo retângulo temos que
Assim pro nosso caso
Resposta
(a)