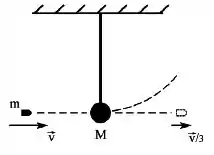
Na figura é representada uma bala de massa e velocidade que atravessa uma esfera de massa pendurada por uma haste de comprimento e de massa desprezível. A bala emerge da esfera com velocidade . Qual é a fração que a energia cinética final representa da energia cinética inicial?
(A)
(B)
(C)
(D)
(E)
Passo 1
O que está acontecendo é que a bala ao colidir coma esfera, sai com uma velocidade menor que a velocidade inicial, entretanto, a esfera que estava parada, agora tem uma certa velocidade que ainda não sabemos.
A questão quer que nós comparemos a energia cinética final com a energia cinética inicial .
Passo 2
Vamos encontrar cada uma dessas energias cinéticas.
Como a esfera estava parada, a energia cinética inicial era apenas a energia cinética da bala:
Já a energia cinética final é a soma da energia cinética da bala com a da esfera:
Sabemos que a bala sai da colisão com uma velocidade de , então conseguimos calcular sua energia cinética :
Porém, ainda não sabemos a velocidade da esfera após a colisão. Achando esse valor conseguimos sua energia cinética e terminamos a questão.
Passo 3
Para achar a velocidade da esfera , vamos utilizar a conservação do momento linear:
Lembrando que o momento linear é dado pelo produto da massa com a velocidade:
Então a conservação fica assim:
Passo 4
Agora que temos , vamos calcular a energia cinética final e achar aquela razão que queremos.
A energia cinética da esfera será:
Então:
Para finalizar vamos calcular e correr pro abraço:
Ficamos com a letra (D).
Resposta
Letra (D)