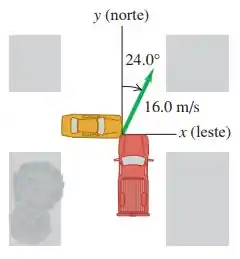
Em um cruzamento da cidade de São Paulo, um carro compacto com massa de que se deslocava de oeste para leste colide com uma picape com massa de que se deslocava do sul para o norte e avançou o sinal vermelho (figura abaixo). Em virtude da colisão, os dois veículos ficam engavetados e após a colisão se deslocam a na direção nordeste. Calcule o módulo da velocidade de cada veículo antes da colisão. Estava chovendo muito durante a colisão, e o atrito entre os veículos e a estrada pode ser desprezado.
Passo 1
Bom dia, boa tarde, boa noiteeee gente linda!! Se tá difícil por aí, deixa que a gente te ajuda. Vamos resolver mais uma com muito ânimo e carinho? Bora lá!!
O enunciado nos fala sobre uma colisão entre um carro compacto e uma picape. Devido a colisão, os dois veículos ficam engavetados, ou seja, basicamente um carro “entrou” dentro do outro. E juntos, esses carros se deslocam a na direção norte. Logo, galerinha temos que encontrar a velocidade de cada veículo antes da colisão. E como vamos fazer isso?

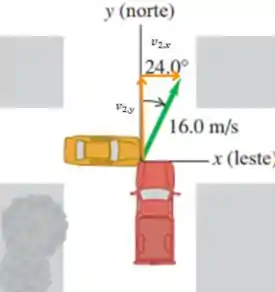
Vamos considerar que o momento linear se conserva, ok? Porque até então a questão não nos deu motivos para acreditar que haja forças externas atuando sobre os veículos. E como os veículos se deslocavam em direções diferentes inicialmente, utilizaremos a conservação do momento linear para cada eixo. Portanto, para o eixo :
Como e o enunciado nos informou que os veículos andam juntos após a colisão, temos que:
Observe que pelo fato da picape se deslocar inicialmente na vertical, essa não possui componente de velocidade no eixo .
Onde:
: massa do carro compacto;
: velocidade inicial do carro compacto em relação ao eixo .
: massa da picape;
: velocidade do conjunto(carro + picape) após a colisão dos mesmos;
Substituindo os valores correspondentes, obtemos que:
E como a princípio o carro compacto só possui velocidade em relação ao eixo . Podemos afirmar que já será o módulo de sua velocidade.
Passo 2
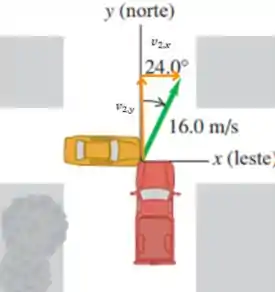
Agora vamos escrever a conservação do momento linear para o eixo . Assim,
Sendo ,
Note que agora quem não possui componente de velocidade em relação ao eixo é o carro compacto, uma vez que, esse veículo antes da colisão se deslocava na direção horizontal.
Logo,
: massa da picape;
: velocidade inicial da picape em relação ao eixo ;
: massa do carro compacto;
: velocidade do conjunto (carro compacto + picape) após colisão;
Substituindo com os valores do enunciado,
E como vimos que a picape só possui componente da velocidade em relação ao eixo .Desse modo, já é o módulo de sua velocidade.
Então foi isso pimpolhos! Com essa questão, esperamos que vocês tenham compreendido um pouco mais sobre colisões e conservação do momento linear. Te esperamos no próximo exercício, beijinhos! 😊