Colisão, Energia Potencial e Conservação de Energia
Dois pêndulos de comprimento estão suspensos juntos conforme a figura abaixo. O pêndulo (de massa ) é solto a partir do repouso de uma altura enquanto que o pêndulo (de massa ) está em repouso na posição vertical.
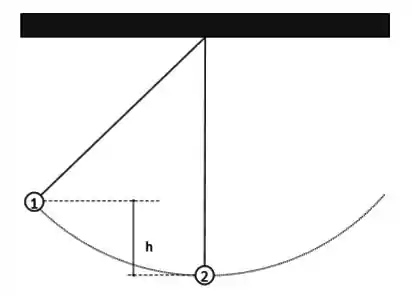
Considerando inicialmente que a colisão é elástica determine:
A velocidade do pêndulo imediatamente antes do choque.
A velocidade de cada pêndulo imediatamente depois do choque.
Supondo agora que a colisão seja inelástica e os dois pêndulos fiquem grudados após a colisão, qual a máxima altura que os dois pêndulos atingem?
Quanta energia foi dissipada na colisão inelástica?
Dado: .
Passo 1
Por conservação de energia:
Tomando o ponto mais baixo como referencial de energia potencial nula e lembrando que o pendulo parte do repouso, portanto :
Passo 2
Visto que o enunciado informou para tratarmos como uma colisão elástica, ou seja, sem perdas de energia. Podemos utilizar conservação de energia cinética e conservação de momento linear.
Por conservação de momento linear:
O Pendulo estava em repouso antes da colisão, portanto .
Por conservação de energia cinética:
Novamente, lembremos que
Ficamos então com o sistema:
Substituindo a primeira equação na segunda temos:
Substituindo agora o na primeira equação do sistema:
Substituindo agora que , e .
Lembrando que:
Passo 3
Como a Colisão agora é inelástica, não poderemos utilizar conservação de energia cinética, apenas conservação de momento linear:
Por conservação do momento linear:
Lembrando que .
Substituindo:
Após a colisão, podemos fazer conservação de energia mecânica:
Substituindo os valores, teremos:
Passo 4
A variação de energia é:
Obs.: A energia deu negativa, pois se trata da energia dissipada(perdida).