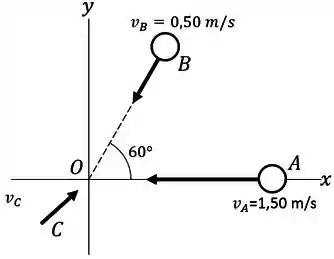
As esferas (massa ), (massa ) e (massa ) se aproximam da origem deslizando sobre uma mesa de ar sem atrito. As velocidades de e são indicadas na figura. Todas as três esferas atingem a origem ao mesmo instante e ficam coladas. Quais devem ser os componentes e da velocidade inicial de para que os três objetos unidos se desloquem a no sentido do eixo após a colisão? Se possui velocidade encontrada no item (a), qual é a variação da energia cinética do sistema das três esferas ocasionada pela colisão?
Passo 1
Temos uma colisão acontecendo, assim a primeira coisa a saber é que o momento linear do sistema é constante.
Ele não define a colisão, mas diz que as esferas ficam coladas, então depois da colisão todas tem a mesma velocidade, isso é o mesmo que falar que a colisão é inelástica.
Passo 2
Vamos escrever cada velocidade que sabemos pelo enunciado
Ambas negativas devido ao sentido do movimento, contra o eixo e . E ainda temos a velocidade final de todas
Passo 3
Para a velocidade do corpo vamos precisar decompor a velocidade usando a “regra do COlado/SEparado”
Então
Passo 4
Vamos calcular o momento linear antes e depois e usar a conservação dele.
Primeiro vamos calcular o momento linear inicial , que é dado por
Agora, vamos calcular o momento linear final
Passo 5
Igualando os momentos lineares vamos ter
Passo 6
Para achar a variação de energia cinética devemos achar a energia do sistema antes e depois.
A energia cinética antes é
Para a energia cinética devemos ter o módulo da velocidade dos corpos, precisamos então achar o módulo da velocidade de
Passo 7
Vamos ter então
Passo 8
Vamos agora achar a energia cinética do conjunto depois do choque
Passo 9
A variação de energia cinética é
Resposta