UFU, Sem Campus, Cálculo 1, Prof° Sato - Listas de Cálculo 1 - 1ª Lista de Exercícios, Questão 3.13a
Considere a função cujo gráfico é dado a seguir e faça o que se pede
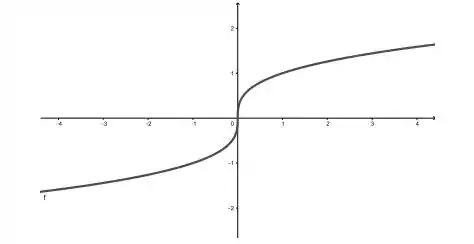
Justifique a afirmação é uma função injetora;
Passo 1
Eaew, belezinha?
A questão nos dá o seguinte gráfico de uma função
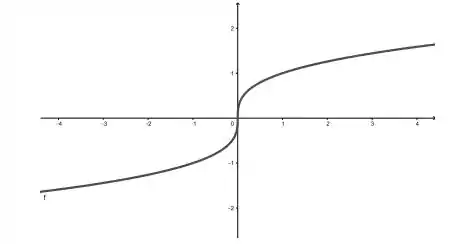
e, esta alternativa pede para argumentarmos se , é uma função injetora! Isso é bastante simples se lembrarmos a definição do que é uma função injetora. Matematicamente, temos que
se e somente se
Mas, e daí? O que isso quer dizer? Vem comigo se não lembrar!
Passo 2
A relação que apresentei no passo indica que para cada valor de existe apenas um resultado para a nossa função. Para você visualizar o caso em que a função não é injetora, vamos analisar a parábola
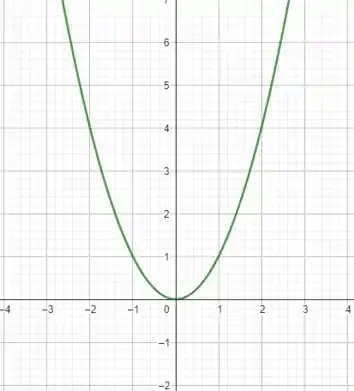
Note que dois valores de diferentes (por exemplo e ) levam ao menos valor , portanto, a parábola não é injetora! Isso pode ser visualizado traçando uma linha horizontal e checando se ela cruza a curva mais de uma vez! Na parábola acima sim! No gráfico de nossa função
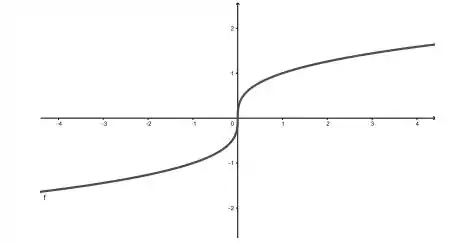
Linhas horizontais cruzam a função apenas uma vez, não importa onde você traça a linha horizontal, portanto, a nossa função é injetora! A primeira alternativa foi isso! Te vejo na próxima! Até já!
Resposta
Ao longo dos passos!