UFES, Sem Campus, Cálculo 1, Listas de Estudos UFES - Cálculo 1 - Lista 10, Questão 30a
Seja .
Mostre que é invertível;
Passo 1
Eaew, tudo certinho contigo?
Precisamos considerar a seguinte função
e nesta alternativa determinar se ela é invertível! Mas o que significa a função ser invertível? A função precisa ser bijetora, ou seja, ser injetora e sobrejetora, dois conceitos intimamente ligados ao domínio e imagem da função! Portanto, vamos usar o gráfico desta função, para determinar se ela é invertível ou não! Bora lá!
Passo 2
Temos que o gráfico da função é dado por
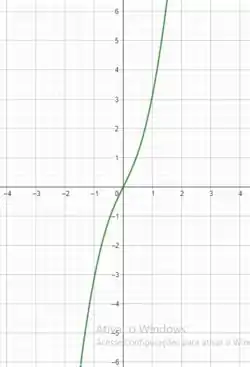
Note que para todo valor de que é o domínio da função , temos um valor diferente pertencente a imagem da função. Sendo assim, ela é injetora! Note que a imagem desta função é todos os , portanto, tendo o domínio da inversa como os ℝ, temos que ela é invertível sem maiores dificuldades!
A primeira alternativa foi isso! Até a próxima!
Resposta
A função é invertível!