Determine a inversa da função
Identifique o domínio e imagem da inversa de , denotada por
Passo 1
Faaaalaa, beleza?? Bora para esse probleminha envolvendo função e sua inversa. Primeiro, há uma forma de enxergamos o domínio e imagem de uma função inversa sem nem calcular ela. Bora ver isso, se temos do tipo:
Daí temos que:
Ou seja, basta a gente entender o domínio e imagem da função . Para fazermos isso, podemos fazer uma análise do gráfico de . Bora ver isso:
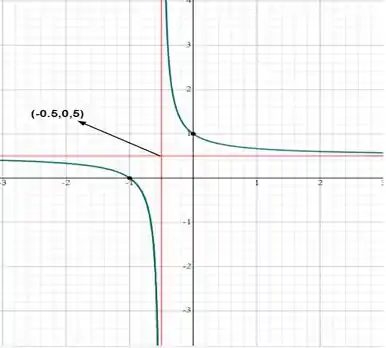
Ou seja, temos que:
Domínio de = Imagem de
Imagem de = Domínio de
Passo 2
A gente já sabe, portanto, o domínio e imagem da inversa, bora agora calcular ela e ver se é compatível.
O processo para calcular a inversa é a seguinte, vamos colocar aonde tá na função e aonde tá , ou seja:
Pelo processo
Agora queremos isolar o valor de , bora “jogar” pro outro lado:
Ou seja:
E por isso:
Dai, temos que:
E agora podemos ver que de fato, o domínio e imagem achados no começo estão certos, uma vez que o gráfico dessa função é:
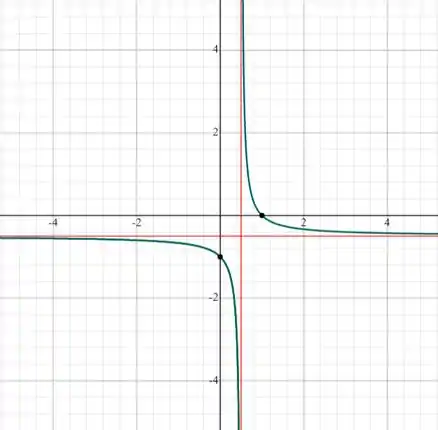
Ou seja, é compatível com o que achamos antes. Agora que acabamos com esse problema, bora para o próximo?
Resposta
Imagem de
Domínio de