UFSCAR, Sem Campus, Cálculo 1, Listas Cálculo 1 - UFSCAR - Tarefa 3 - Fundamentos de Probabilidade, Questão 3
Nos itens a seguir são representados, em diagrama de flechas ou no plano cartesiano, os gráficos de algumas funções. Classifique-as em injetora, sobrejetora ou bijetora. Justifique suas respostas.
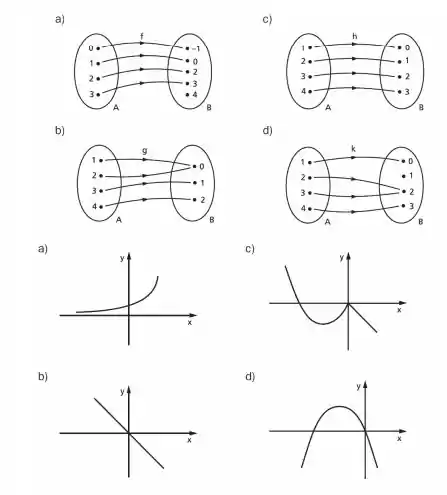
Passo 1
Oiiie, tudo bem?
Precisamos comparar as funções dadas nas alternativas, algumas foram definidas apenas em relação de um conjunto domínio e um conjunto contradomínio. Assim como também é dado o gráfico das funções! Devemos usar essas informações para saber se a função é injetora, sobrejetora e bijetora. Você lembra quais são as definições?
- Uma função injetora tem para cada item de seu domínio um valor diferente em seu contradomínio.
- Uma função sobrejetora tem o seu contradomínio igual à sua imagem (ou seja, o gráfico passa sem saltos por todo o contradomínio).
- A função bijetora é tanto injetora quando sobrejetora!
Usando isso, vamos analisar as nossas alternativas! Vem comigo!
Passo 2
Temos primeiro a seguinte função definida no diagrama de flechas e plano cartesiano
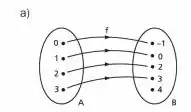
Essa função é injetora, pois todos os itens no conjunto levam a um item diferente no conjunto , mas não é sobrejetora, pois existe um item no contradomínio que não está presente na imagem! Como ela não é sobrejetora, ela não é bijetora! Vamos para a próxima!
Passo 3
Temos agora que
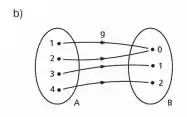
A função não é injetora por dois itens do conjunto levam para o mesmo valor no conjunto . Ela é sobrejetora pois todos os itens do contradomínio fazem parte da imagem! No entanto, como não é injetora, ela não é bijetora! Vamos para a próxima!
Passo 4
Temos agora que
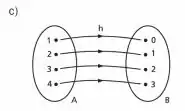
Pelo diagrama de flechas essa seria uma função injetora, mas note pelo gráfico que dois valores de podem levar ao mesmo valor de , portanto, ela não é injetora! Ela é sobrejetora, no entanto, já que o contradomínio está completamente ocupado! Essa função não é bijetora! Falta só mais uma!
Passo 5
Para última, temos
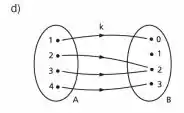
A função não é injetora, e também não é sobrejetora! Note que dois valores de levam para o valor . e, que o valor não está ocupado! A função não é bijetora!!
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Injetora, não-sobrejetora, não-bijetora
não-injetora, sobrejetora, não-bijetora
não-injetora, sobrejetora, não-bijetora
não-injetora, não-sobrejetora, não-bijetora