Sejam dados e conjuntos não vazios.
- Defina rigorosamente o conceito de função de em
- Defina rigorosamente os conceitos de função injetora, sobrejetora e bijetora.
Passo 1
Letra
A definição rigorosa de função é a seguinte
Dados dois conjuntos e , uma função de em é um subconjunto de , portanto uma relação entre e satisfazendo a seguinte propriedade
Para todo , existe um único elemento tal que
Moleza né? Próxima rs
Gente, calma. Não vamos fazer isso com vocês, além de colocarmos a definição vamos entende o que ela significa tá?
Vamos considerar dois conjuntos e
A relação entre eles é conectarmos elementos de em elementos de , como por exemplo
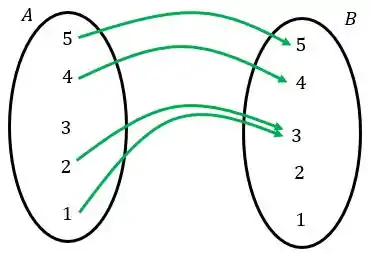
Estamos relacionando o com o , o com o , o com o e o com o .
A função é quando, TODO elemento de está relacionado a APENAS UM elemento de com alguém.
Essa relação verde não é função porque o não tem relação com ninguém.
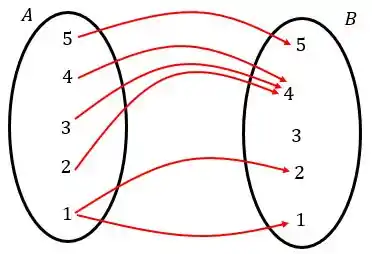
Nessa relação vermelha, todos os elementos de tem uma relação, mas o está relacionado com o e com o ao mesmo tempo, então também não teremos uma função.
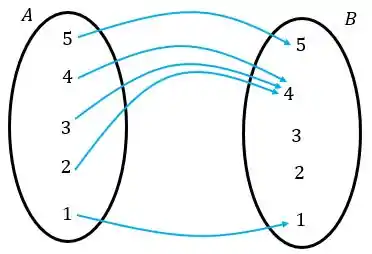
Agora essa relação azul é uma função, porque todos de tem relação e está ligados a um único elemento de . Não tem problema o estarem ligados no mesmo elemento de , desde que eles estejam ligados a um elemento só de
Passo 2
Vamos primeiro para a função injetora
Uma função é injetora se para qualquer para de elementos distintos do domínio, suas imagens são também distintas.
Em outras palavras, , com , temos
Podemos ver isso de outra forma também, que é a contrapositiva , com então
Mas o que isso significa?
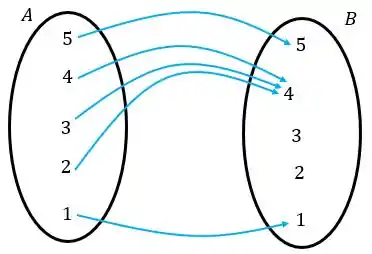
Essa função não será injetora, porque para ser injetora cada elemento de deve estar ligado a um diferente elemento de .
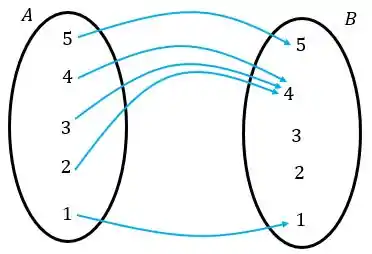
Essa agora vai ser uma função injetora.
Passo 3
Vamos agora para a função sobrejetora
Uma função é sobrejetora se a imagem coincide com o contradomínio. Ou seja, se todo elemento de possui uma relação com algum elemento de
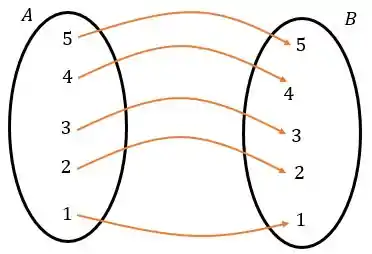
Essa nossa função azul não é sobrejetora, porque o e o estão em mas não possuem relação.
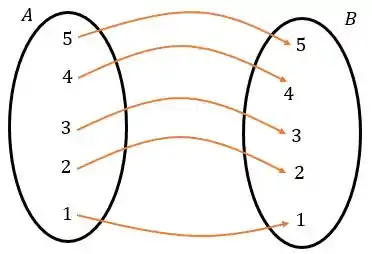
Agora sim, todos os elementos de tem relação com o de
Passo 4
A função bijetora é uma função que é injetora e sobrejetora ao mesmo tempo.
Como a nossa função laranja
Resposta
Ei, a resposta está no passo a passo :)