UFSCAR, Sem Campus, Cálculo 1, Listas Cálculo 1 - UFSCAR - Tarefa 3 - Fundamentos de Probabilidade, Questão 4c
Mostre que as funções definidas são bijetoras e determine a sua função inversa.
tal que .
Passo 1
Eaew, tudo certinho contigo?
Temos a seguinte função
tal que
precisamos mostrar que ela é bijetora (injetora e sobrejetora), e achar a sua inversa! As condições para ser injetora e sobrejetora são
- Uma função injetora tem para cada valor de um valor de .
- Uma função sobrejetora tem contradomínio igual a sua imagem.
- A função bijetora é tanto injetora quando sobrejetora
Vamos precisar verificar as condições acima! E encontrar uma função , tal que
Vamos lá!
Passo 2
Temos que nossa função é dada por
Vamos dar uma olhada no gráfico desta função, temos que
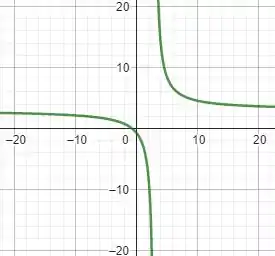
Perceba que não há dois valores de em que seja igual! Portanto, ela é injetora! Ela também é sobrejetora já que o contradomínio ℝ está todo presente na imagem! Portanto, ela é bijetora! Vamos ver se conseguimos encontrar uma inversa!
Passo 3
Queremos uma função composta
Essa relação nos dá que
podemos multiplicar os dois lados por , para obter que
Isolando , temos que
ou simplesmente
Como não está no contradomínio de , essa função está bem definida! A alternativa foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Ao longo dos Passos!