UFSCAR – Cálculo 1 – Lista 1 – Revisão de Funções – 5a
Encontre uma fórmula para a função inversa
a)
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado pediu pra gente uma fórmula para a inversa da função . Mas o que é uma inversa?
Uma função inversa, como o nome já sugere, é uma função que faz o inverso da função . Como assim? As funções inversas “revertem” umas as outras. Por exemplo, se leva para , então a inversa, , deve levar para :
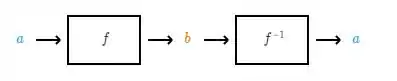
Ou, em outras palavras, .
No nosso caso, nós temos a lei de formação da função:
E nós precisamos encontrar . Como fazemos isso? Nós vamos chamar e encontrar a entrada de que corresponde a uma saída . Quer dizer, vamos trocar e de lugar inicialmente, e então isolar para escrever a inversa em forma de função. Vamos lá!
Passo 2
Da nossa função , vamos chamar :
Trocando por , temos:
Agora o que podemos fazer pra isolar ? Podemos primeiro subtrair dos dois lados:
E pra remover a raiz, podemos elevar os dois lados da equação ao quadrado:
Agora podemos reescrever como e aplicar a propriedade distributiva, multiplicando termo a termo:
Agora vamos mover todos os termos que não contém para o lado direito da equação:
Simplificando dividindo cada termo por , temos:
E encontramos a nossa inversa:
Prontinho, galera! Encerramos o exercício. 😉