Determine o valor de em de modo que a função de em definida por seja SOBREJETORA.
Passo 1
Para que a função seja sobrejetora, precisamos que a imagem seja igual ao contradomínio. Lembrando que o contradomínio é o conjunto que contém todas as imagens possíveis para a função.
Então o que a questão pede é achar quis valores de que satisfaçam isso. A gente vai fazer isso olhando o gráfico.
Passo 2
Vamos observar o gráfico da nossa função.
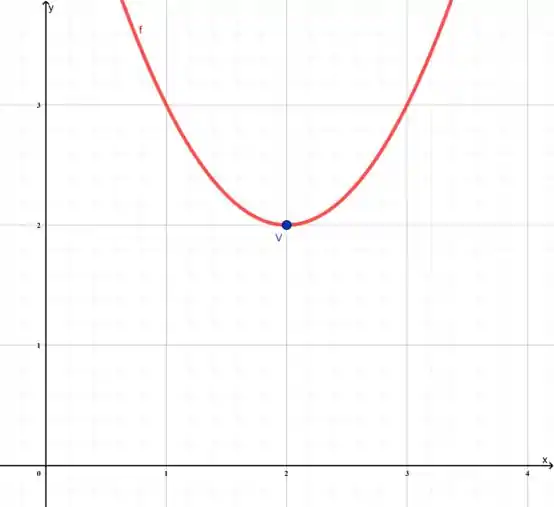
Perceba que o nosso vértice está no ponto , ou seja o nosso domínio(x) só atingirá valores maiores do que 2 no contradomínio. Vê se assim fica mais claro:
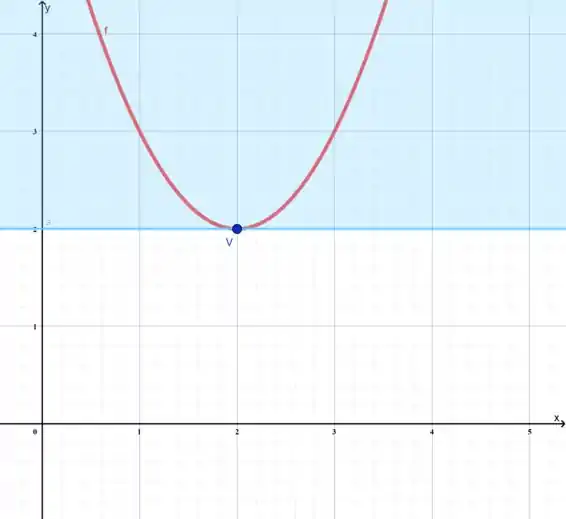
Isso significa que para a Imagem ser igual ao contra domínio, o nosso b precisa ser maior ou igual a 2.