8. Seja . Em qual dos domínios abaixo é injetora?
Passo 1
Oi, galerinha! Tudo bom? Aqui nós temos que achar o intervalo do domínio de uma função, onde ela será injetora.
Para quem não lembra, uma função é injetora se para dois pontos quaisquer pertencentes ao domínio de :
Tivermos:
Ou seja, temos que achar o domínio, onde para uma não exista mais de um possível.
Agora bora analisar!
Passo 2
Nossa função é o módulo de uma equação do segundo grau.
O perfil do gráfico de uma equação de segundo grau é uma parábola, ou seja, essa função só seria injetora em uma metade da parábola.
Para visualizar melhor a parábola, vamos fazer o gráfico da função .
Primeiro, vamos achar
Agora vamos achar os pontos onde . Para isso, vamos aplicar Bhaskara,
Logo, a função intercepta o eixo em
E
O gráfico ficaria assim,
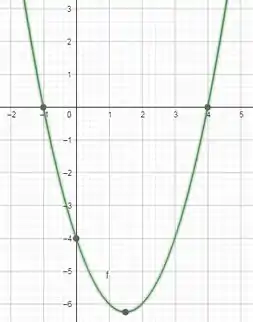
Mas, então, galerinha, nós temos uma função módulo! Logo toda essa parte negativa (abaixo de do eixo ) será positiva.
Então nossa função ficará assim:
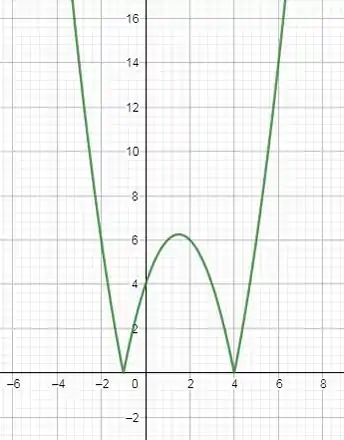
Passo 3
Agora que já conhecemos a cara da função, temos que dizer onde que é o domínio da parte injetora (ou seja, que só tenhamos uma para cada )
Repara então que a nossa função so sera injetora nas seguintes regiões:
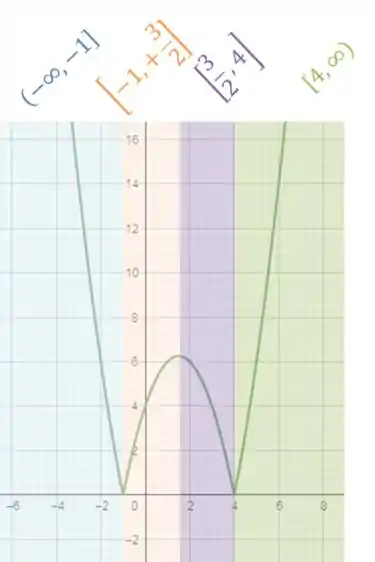
Logo, pelas opções disponíveis o nosso domínio será .