Para as funções em representadas abaixo qual é injetora? E sobrejetora? E bijetora?
Passo 1
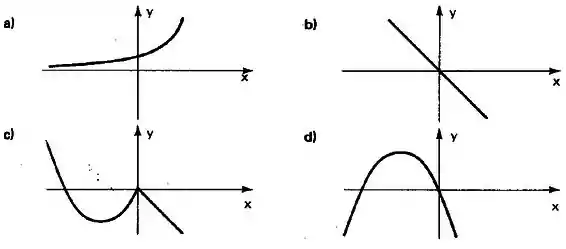
a) A primeira função não é sobrejetora, pois ela não vai atingir todos os valores do contradomínio, nunca atingirá os elementos em y que são menores ou iguais a 0, ou seja a imagem não será igual ao CD.
No entanto, ela será injetora, pois todos os elementos do domínio (x) vão se relacionar a um elemento diferente do contradomínio (y).
Passo 2
b) Essa será bijetora, ou seja injetora e sobrejetora ao mesmo tempo. A imagem é igual ao CD e nunca dois elementos do domínio (x) vão se relacionar a um mesmo elemento do CD (y)
Passo 3
c) Será sobrejetora, pois atingirá todos os elementos possíveis do contradomínio. Mas não será injetora pois existem elementos do domínio que vão atingir o mesmo elemento no contradomínio. Observe só:
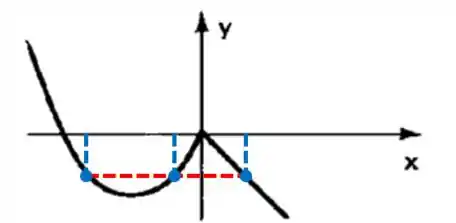
Viu?
Para 3 valores distintos de x, temos o mesmo valor de y associado. Toda vez que mais de um elemento x estiver associado a um mesmo y, você já pode concluir que essa função não é injetora.
Passo 4
Essa não será nem sobrejetora e nem injetora, observe bem:
- Ela não atingirá todos os elementos de y, pois tem um ponto de máximo. Ou seja, a imagem não será igual ao contradomínio.
- Ela tem valores de x que atingem o mesmo y.
Passo 5
Resposta
- Injetora
- Bijetora
- Sobrejetora
- Nem sobrejetora e nem injetora