A matriz tem dois autovalores distintos. Um deles é 2.
(I) O outro autovalor é -2.
(II) O conjunto gerado pelos autovetores associados ao autovalor 2 tem dimensão 1.
(a) Ambas as afirmações são falsas.
(b) Ambas as afirmações são verdadeiras.
(c) (I) é verdadeira e (II) é falsa.
(d) (I) é falsa e (II) é verdadeira.
Passo 1
Vamos calcular os autovalores da matriz A.
Para isso temos que encontrar as raízes do polinômio característico
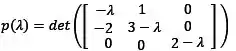
Calculando o determinante e igualando a zero:
Daí temos:
Ou:
ou
Passo 2
Agora vamos calcular os autovetores associados a .
Para isso, aplicamos a definição de autovetor e autovalor:
Então ficamos com o sistema:
Da primeira equação, tiramos que:
Então podemos reescrever nossos autovetores como:
Separando as variáveis:
Isso significa que os autovetores são na verdade o espaço gerado pelos vetores e , isto é:
Como esse conjunto tem 2 vetores LI, a dimensão dele é 2.
Passo 3
Agora podemos ver as alternativas.
(I) O outro autovalor é -2.
Isso é falso. O outro autovalor distinto de 2 é o 1.
(II) O conjunto gerado pelos autovetores associados ao autovalor 2 tem dimensão 1.
Essa alternativa também é falsa, pois acabamos de ver que esse conjunto tem dimensão 2.
Resposta
(a) Ambas as afirmações são falsas.