A soma dos MÓDULOS dos autovalores da matriz
é:
(a) 5
(b) 6
(c) 7
(d) 8
Passo 1
Para encontrar os autovalores de uma matriz, precisamos encontrar as raízes do polinômio característico:
onde A vai ser a matriz dada no enunciado.
Passo 2
Vamos determinar primeiro quem é a matriz .
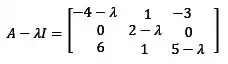
Agora podemos calcular o determinante dessa matriz igualar a zero:
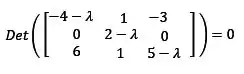
Colocando o termo em evidência:
Daí temos:
ou:
Daí tiramos que:
ou
Passo 3
Encontramos os autovalores:
Somando os módulos deles:
E a resposta está na letra (a).
Resposta
(a) 5
Exercícios de Livros Relacionados
Determinar valores próprios do operador linear T : V → V do R 4 que é definido em uma base { e 1 ,..., e n } por T e i = λ i ∈ R .
Achar os valores e os vetores próprios do operador T do IR 2 dado por:T(x, y) = (x + y, x - y);
Calcular o polinômio característico e os valores próprios da matriz: 2 1 0 0 0 2 0 0 0 0 1 1 0 0 - 2 4
Seja 1 1 0 1 a matriz de um operador do R 2 . Ache os valores próprios de T . Existem, neste caso, dois vetores próprios linearmente independentes?
Provar que se λ é valor próprio de T, então λ n é valor próprio de T n . Generalizando, se p(t) é um polinômio então p ( λ ) é valor próprio de p(T), onde p T =a 0 1+ a 1 T+ . . .+a n T n se p ( t )=a